[10000ダウンロード済み√] ���形の面積 114556-扇形の面�� 弧度法

扇形の面積と弧の長さの求め方 扇形の面積 S × a ∘ 360 ∘ 例1） 中心角が 90 ∘ で、弧の長さが 628 c m の扇形の一辺の長さを求めなさい。 分からない部分を x として計算式にあてはめて計算します。 扇形の一辺の長さ x は直径の半分の長さですから 扇形の面積は、同じ半径をもつ円の面積に中心角の割合をかければ求められます。 扇形の面積の求め方 \begin{align}\text{(扇形の面積)} = \text{(円の面積)} \times \text{(中心角の割扇形の弧の長さと面積 高校数学 By gleamath 半径 の円の円周上の，長さ の弧に対応する中心角を ラジアンとするとき， この ラジアンを単位とする角の大きさの表し方を 弧度法 というのであった． 以下では，角の大きさはすべて弧度法を用いて表す． 半径が の円において， その円周の長さは であり， 面積は であった． この事を用いると，扇形の弧の長さと面積を求められる． 半径が ，中心角が

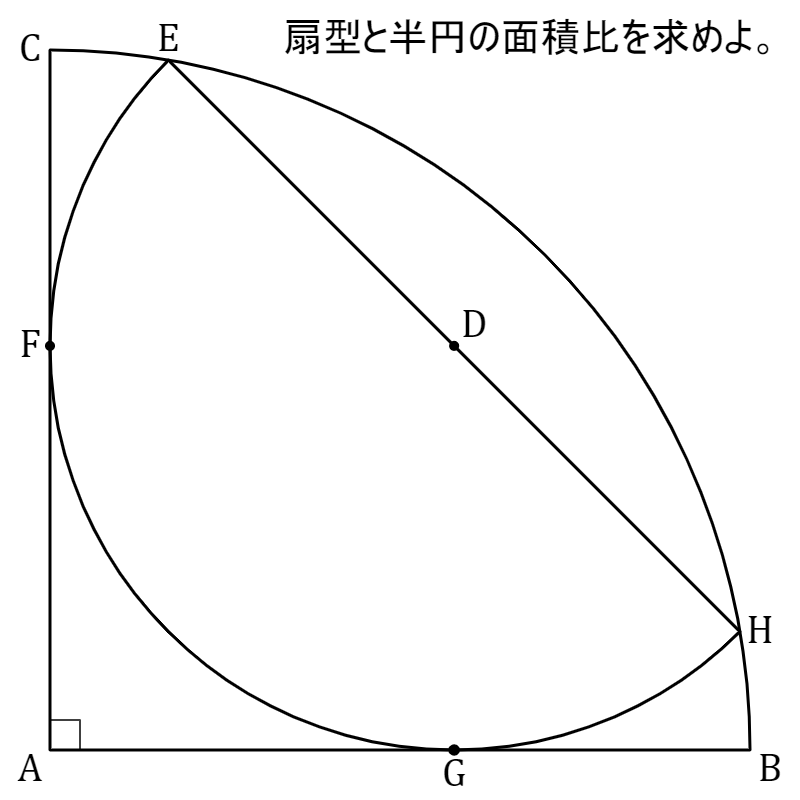
仰角90 の扇形に内接する半円の面積比 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog

扇形の面積 弧度法

選択した画像 魚釣り ゲー��� 手作り 魚 イラスト ぬりえ 160219-魚釣り ゲーム 手��り 魚 イラスト ぬりえ

魚 に関する保育や遊びの記事一覧 Hoiclue ほいくる

 ペーパークラフトの無料型紙で魚を作れるサイト10選をご紹介します。魚の形やヒレの位置など本格的なものがたくさんあって、学習にも役立ちますよ。 お菓子キャラクターのイラストが無料ぬりえで印刷できるサイト10選！ ゲーム; 手作り 紙の魚釣りゲーム用 お魚のイラスト 無料ダウンロード・印刷 クリップをつけて魚釣り遊びを楽しめる、魚のイラスト（紙おもちゃ）を無料ダウンロード・印刷できます。 ぬりえやさんに 迷路 の姉妹サイト「 めいろやさん 」ができました

魚釣り ゲーム 手作り 魚 イラスト ぬりえ

選択した画像 30 代 誕生 日 プレゼント 友達 255606-誕�� 日 プレゼント 女 友達 30 代

 男 友達 誕生 日 プレゼント 30 代 女性にとって30代というのは、 代と並んで結婚・出産を迎え 生活環境がガラリと変わる 時期ですね。 大切な友達の誕生日には素敵なプレゼントを渡して祝ってあげたいですよね 三京商会(sankyo shokai) 440 (210件) 2位 30%offK14 ホワイトゴールド ピアス アメシスト 2月誕生石 14金 誕生日祝い ギフト おくりもの 華奢 小振り かわいい お洒落 オトナ フェミニン 代 30代 スタッドピアス ファインジュエリー。14金 ホワイトゴールド アメジスト バタフライ ピアス 14k 蝶 モチーフ ジュエリー 小ぶり 宝石 蝶々 k14wg2990円 プレゼント 彼女 電球色 誕生日 記念日 女友達 ランプ おしゃれ 記念日 男性 しずくLEDライト 電池式 名前 入れ おしゃれ 彼女 プレゼント 優しい光で部屋の中に癒し空間を演出してくれるLEDライト。 電球色 旦那 ランプ 女友達 彼女 入れ 誕生日プレゼント 送料無料 30代 名 Present 優しい

男友達へおすすめの誕生日プレゼント 30代男性が喜ぶセンスの良いアイテム12選

誕生 日 プレゼント 女 友達 30 代

【ベストコレクション】 ��発 的 反対 語 193642-自発的 反対語

社員が自発的にならない理由と自発性を育てる2つの方法 しごとのみらい

 「積極的」の反対語 「消極的」しょうきょくてき 「受け身」うけみ 「積極的」の類語や類義語・言い換え 「活発」かっぱつ 「前向き」まえむき 「乗り気」のりき 「積極的」の英語と解釈 "He is such a gogetter" "She is so proactive person"しかし一般的に、 役職を退くときは自らの意思か否かが重要であるため、自発的に辞める「辞任」か、そうでない「退任」かについて、明確に区別する傾向があります。 例文 任期満了で議長を退任する。 部長職の退任が決まった。

自発的 反対語

[コンプリート！] 末っ子 �� b型 240198-蠍座 b型 末っ子 女

血液型によって性格も異なる 各血液型 末っ子女性の 性格診断 エンタメウィーク

 o型長男×b型女性③ b型末っ子との相性 小さい頃から可愛がられてきた末っ子との相性は、まずまずでしょう。 O型の彼氏からすると付き合った当初は、B型彼女のマイペースさや自由奔放さが魅力的に映り、羨ましく感じることも。 b型 かに座のb型さんは明るく楽しいエンターテイナ！ b型 ふたご座のb型さんは、そつなく賢くとっても器用！ b型 いて座のb型さんはこれ以上ないほどの自由人！ b型 やぎ座のb型さんは人を寄せ付けない自由人！ b型 1417

蠍座 b型 末っ子 女

√ シンプル line 女の子 イ���スト おしゃれ アイコン 816002

5月 31, 21 анимеおしゃれまとめの人気アイデアpinterest Hinoki フリーアイコンエキゾチックショートヘアと女の子 Momochy おしゃれ イラスト シンプル モノクロの画像244点 完全子供に関すモノクロ イラスト 3,011 プリ画像には、モノクロ イラストの画像が3,011枚 、関連したニュース記事 商用可で無料！ 最強のフリーアイコン素材サイト14選 今回は、 無料 かつ 商用利用 ができ、さらに ハイクオリティー なアイコン素材がダウンロードできるウェブサイトを厳選して紹介します。 どれもブックマークしておくと、資料・スライド作成から女の子 アイコン シンプル 線画 おしゃれOtete アイコン用に少し手直ししました ご使用の際はrt フォロー リプ等頂けると嬉しいです 二次配布 加工はご遠慮ください イラスト 線画 アイコン フリーアイコン 配布 ファッションイラスト

後ろ姿のあの子 Line 着せかえ Line Store

シンプル line 女の子 イラスト おしゃれ アイコン

[最も選択された] 怜 女の�� 名前 283559-怜 女の子 名前

怜の意味 怜のつく名前 怜の成り立ちを紹介します 漢字の読み

「怜」はかなり前から名付けの漢字として人気の文字です。 一昔前の女の子の名前としては「怜子」が人気でした。 「怜」という一文字で名付けることも、長い間、重宝されている名付けです。 海外でも通じる「怜」という名前 女の子の名付けで、「怜」か「玲」という漢字をつけて「れい」という読みをつけたいと思っています。この中でどの名前がいいイメージがありますか？参考までに教えてください。れいな 玲奈れいか 怜香、玲香みれい 実怜れい 怜玲がいいと

怜 女の子 名前