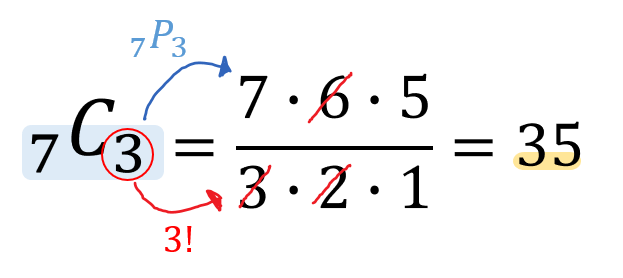
苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ
(α)全員が1つの部屋へ行く 3通り (β)全員が2つの部屋に行く、2^6=64通り ※ここでβは全員が1つの部屋に行くαの場合を重複して計算してしまっているので、2通りを引く。 そしてどの二部屋かを選ぶ3C2=3通り を引くと、 729(3186)=540(通り)// 計算式 7*6*5*4=840 と求めることもできます。 ②答えは432です。 男性から2を選ぶのは組み合わせで =combin(4,2) で 6通りあります。 女性3人から2人を選ぶのは =combin(3,2) で 3通りあります。 選んだ4人の並び順は順列で =permut(4,4) で24通りあります。
組み合わせ 何通り 計算
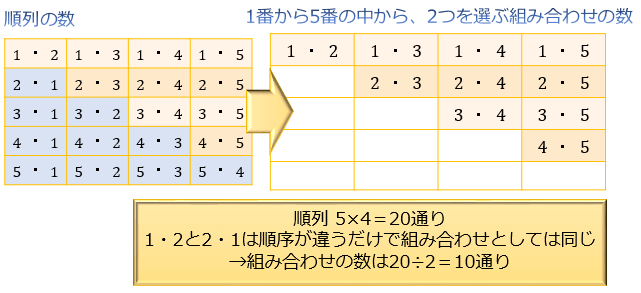
組み合わせ 何通り 計算- nCr（組み合わせ）の意味 組み合わせ C は、 順番を指定しないときの場合の数を求める ときに使います。 しかし、計算するときは一度、 選び方の順番を決めた上で総数を求め、 そのあと重複する数で割って答えを求めるという流れ です。 前章の例題を4 組み合わせの計算問題 それでは、ここから練習として 7 つの問題を解いてみましょう。 これらの 7 つに順番に取り組んで頂ければ、組み合わせ計算に必要な考え方を、ひとつずつステップバイステップで身につけることができるようになっています。
算数 場合の数の解き方は 問題別に考え方を解説 数スタ
win5 組み合わせ点数計算webアプリ 7重勝単式対応 片手でWIN5の組合せ点数計算ができるウェブアプリです。 重勝単式投票で何通りが必要になるかの購入点数の確認に。 電卓みたいに数字ボタンを押すだけで計算されます。 スマホなら「表示固定」ボタンで 競馬ボックス何通り？ 計算式 全券種解説 最終更新日： うまめしcom 競馬必勝法の北村です。 ボックス点数早見表 競馬で馬券を買う時にボックス買いの組み合わせ数が何通りかすぐわかるように早見表を作ってみました。 確率や組み合わせの計算って面倒だしなかなか難しいと思います。 そこで今回は、ロト6は何通りの組み合わせがあるのか？ 当せん確率や期待値はどれくらいなのか？ などを実際に計算してみました！ 結論としては 全部の組み合わせは6,096,454通り 1
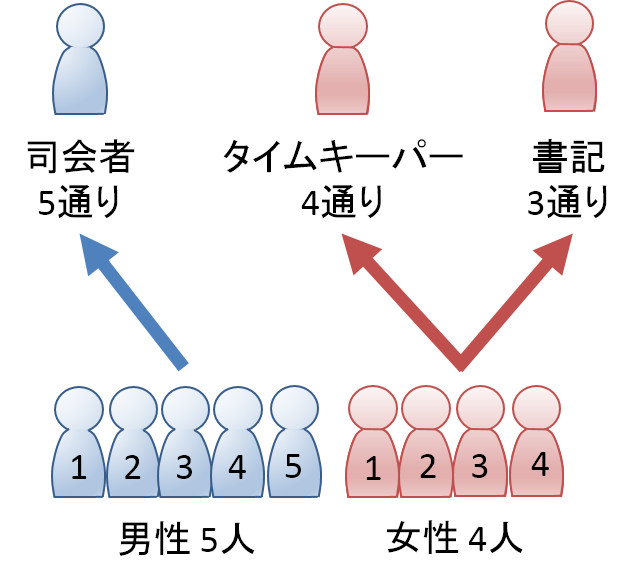
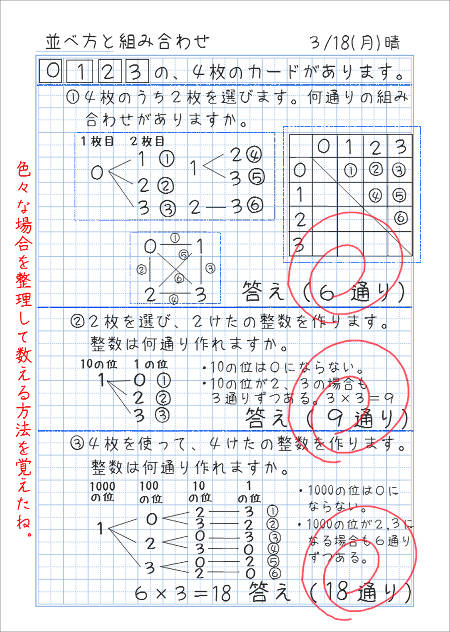
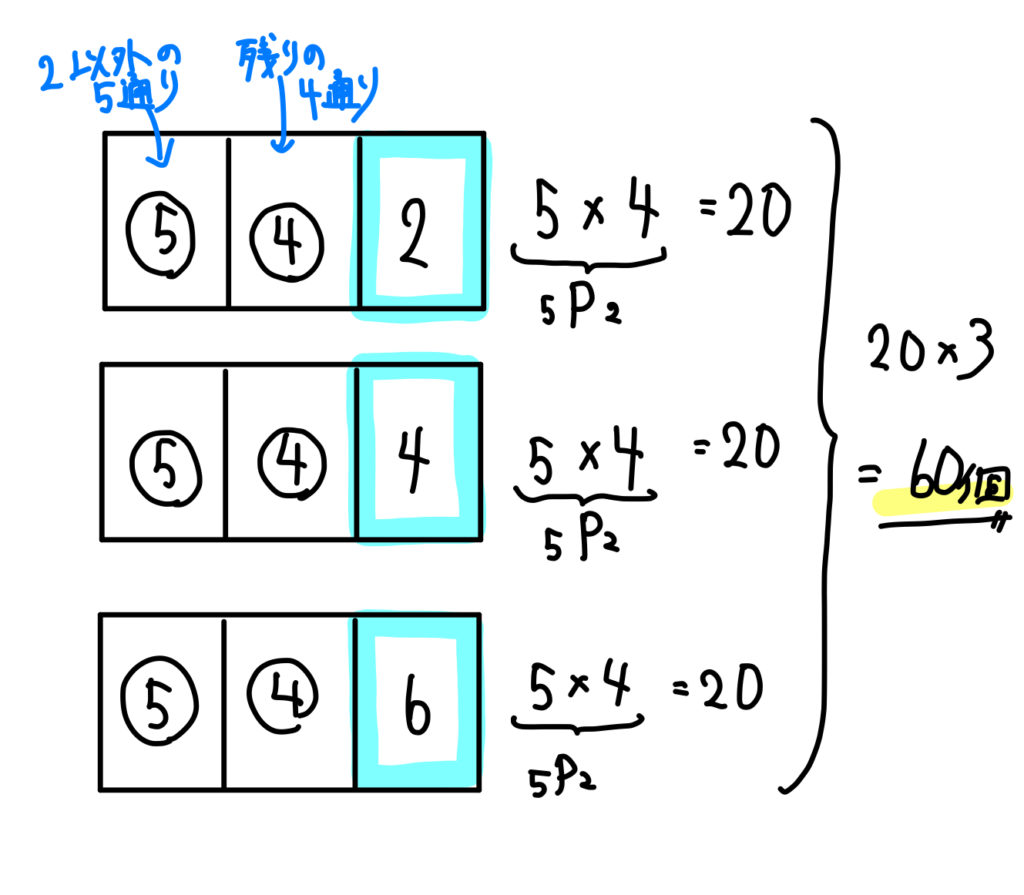
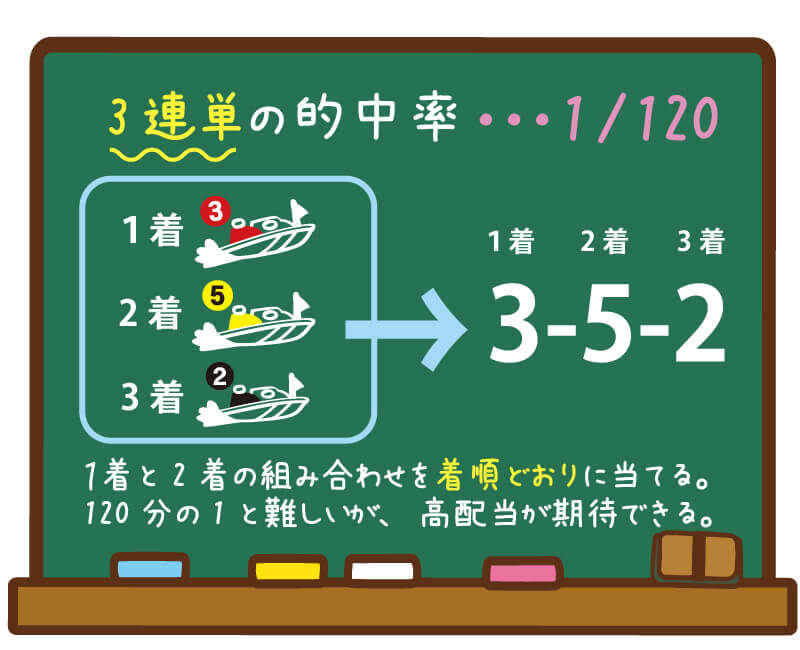
組み合わせは全何通り？ 競艇は6艇で競われる競技のため、3連単の組み合わせは全部で1通り。 このことから、3連単が当たる確率は 08%（1/1） となり、的中させることが難しい玄人向けの買い方と言えるでしょう。 確率（的中率）の底上げは可能 今回は、組み合わせパターンを調べる関数をご紹介します。 組み合わせパターンを調べる 例えば、14種類のデータがあったとして、その中から3つを1セットとした場合、全部で何通りのパターンが考えられるか？ combin関数での引数の指定 総数：種類の立候補した5人の中から 図書委員を2名 決める時、何通りが考えられるか。 「0」「1」「2」「3」と書かれた紙がそれぞれ1枚ずつあり、これらから 3枚の紙を選ぶ時 、何通りの選び方があるか。;
組み合わせ 何通り 計算のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 順列と組み合わせの公式とその違い 問題付き 理系ラボ | 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ | 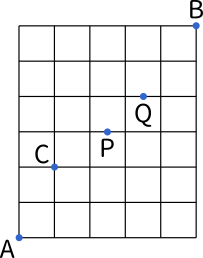 順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ | 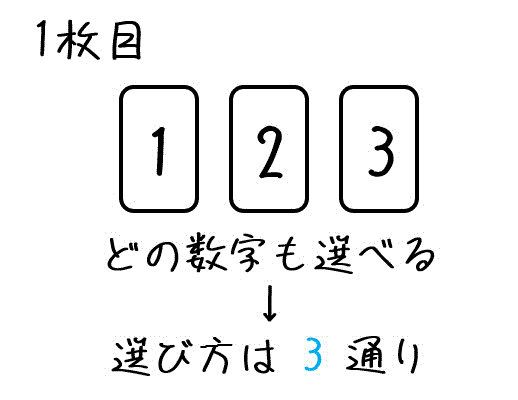 順列と組み合わせの公式とその違い 問題付き 理系ラボ |
「組み合わせ 何通り 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ | 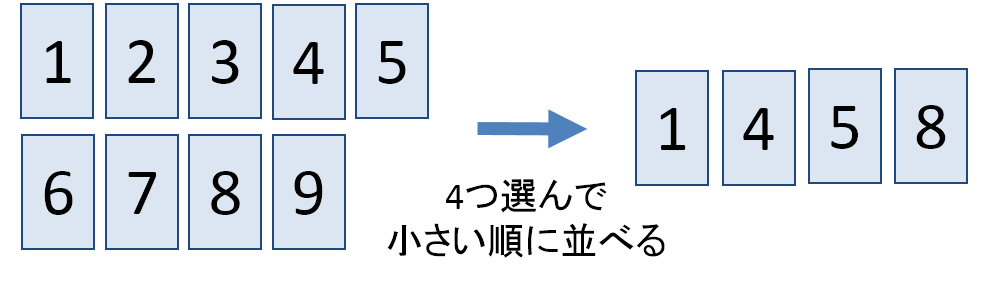 順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ | 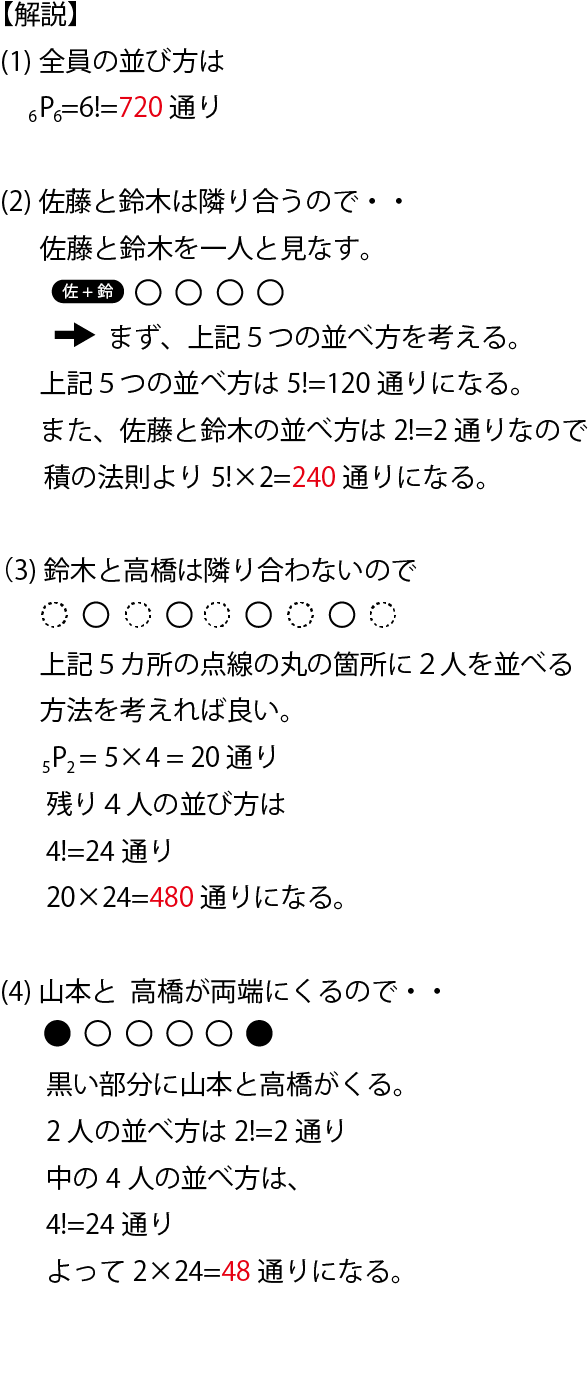 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
「組み合わせ 何通り 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
「組み合わせ 何通り 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 順列と組み合わせの公式とその違い 問題付き 理系ラボ | 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
「組み合わせ 何通り 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
「組み合わせ 何通り 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
「組み合わせ 何通り 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ | 順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ | 順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
「組み合わせ 何通り 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ | 順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ | 順列と組み合わせの公式とその違い 問題付き 理系ラボ |
「組み合わせ 何通り 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 順列と組み合わせの公式とその違い 問題付き 理系ラボ | 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ | 順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
「組み合わせ 何通り 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
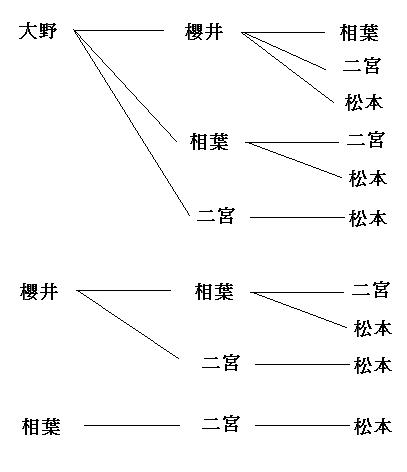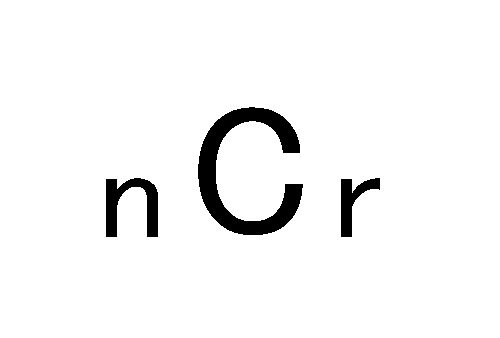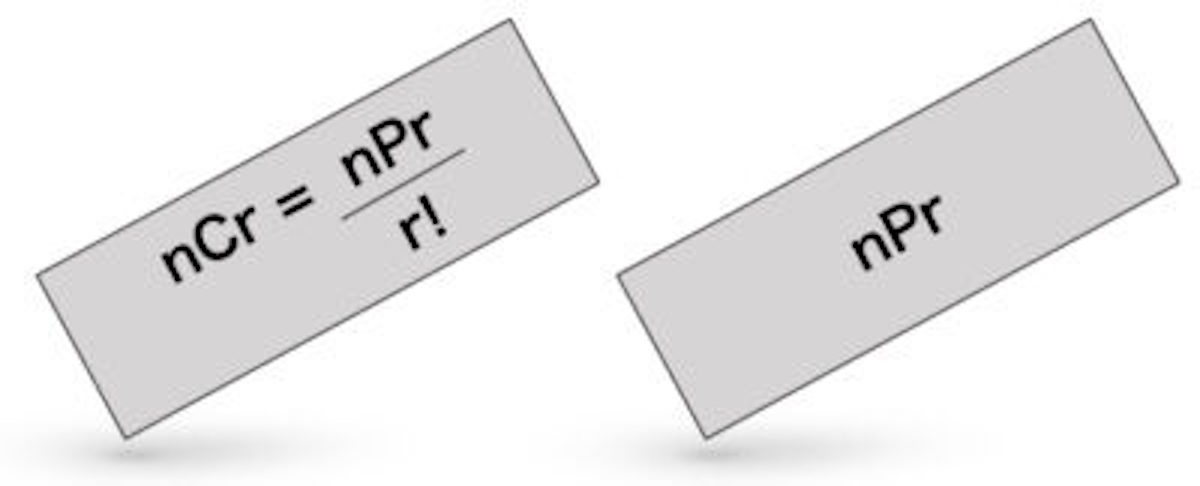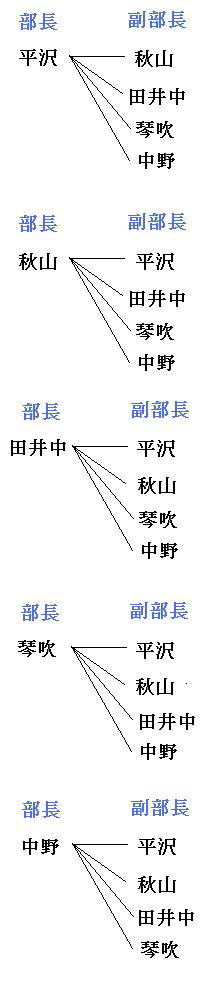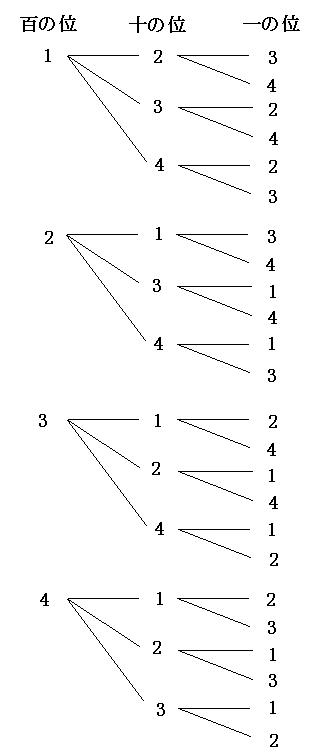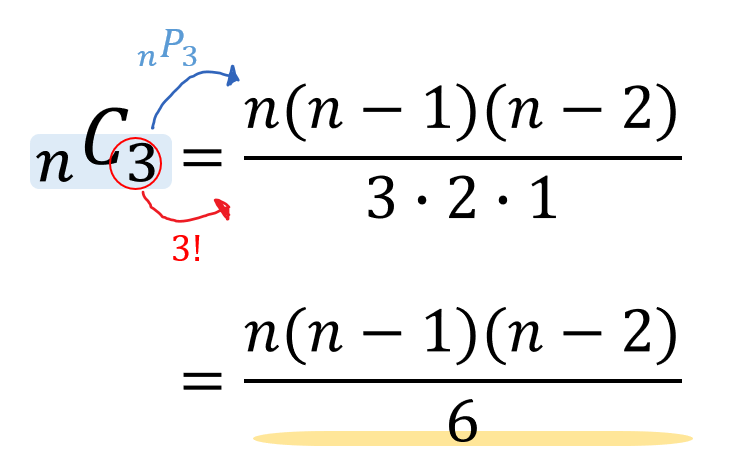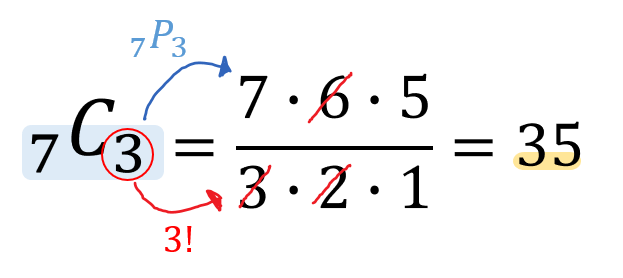 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |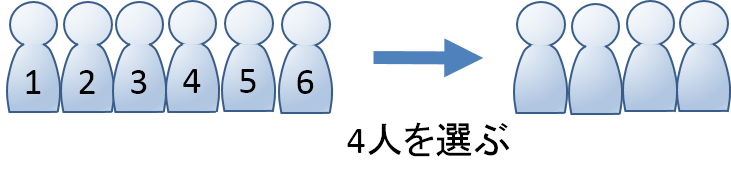
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ | 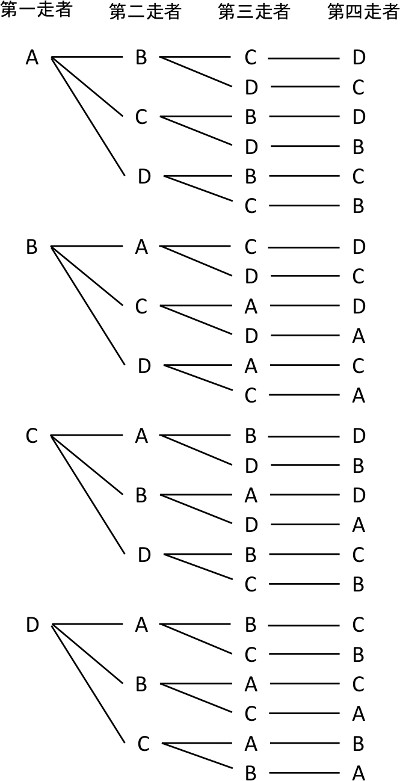 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
「組み合わせ 何通り 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ | 順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ | 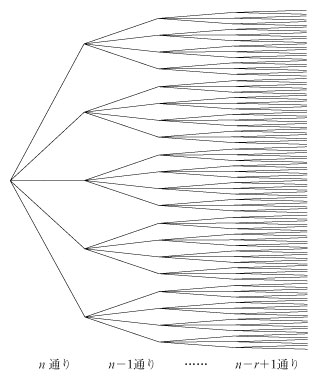 順列と組み合わせの公式とその違い 問題付き 理系ラボ | 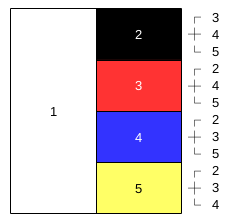 順列と組み合わせの公式とその違い 問題付き 理系ラボ |
「組み合わせ 何通り 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |  順列と組み合わせの公式とその違い 問題付き 理系ラボ |
 順列と組み合わせの公式とその違い 問題付き 理系ラボ | 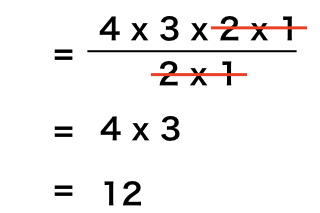 順列と組み合わせの公式とその違い 問題付き 理系ラボ |
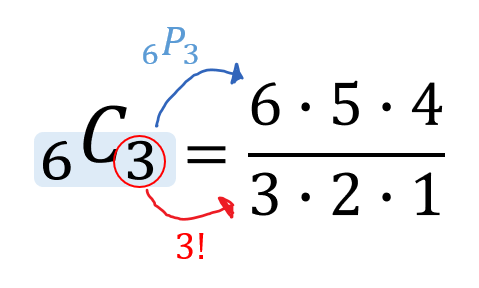
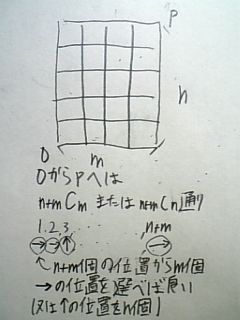
組み合わせの計算方法の証明 順列では、「並べる」という操作が入りますが、組み合わせでは「並べる」という操作は除外されます。 例えば、1, 2, 3の三つの数字について、順列の全ての場合を列挙すると次の6通りがあります。よって24通りです。 例題 (組み合わせ) 次の組み合わせは何通りか。 ①7人から3人を選ぶ選び方 男子5人、女子2人の中から男子2人、女子1人を選ぶ選び方 解答 ①\(_7 C_3 =\frac{7⋅6⋅5}{3⋅2⋅1}=35\) よって35通りです。
Incoming Term: 組み合わせ 何通り 計算, 組み合わせ 何通り 計算方法,
0 件のコメント:
コメントを投稿