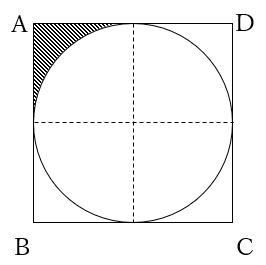
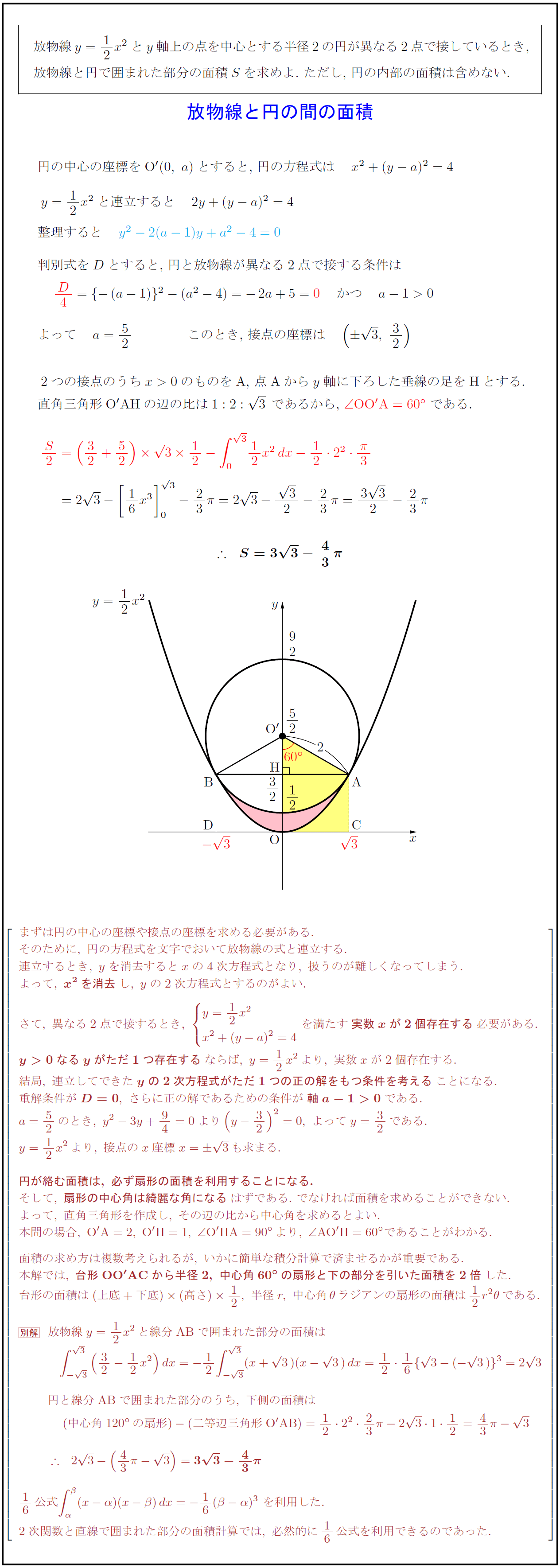
円と帯の共通部分の面積 Den Of Hardworking
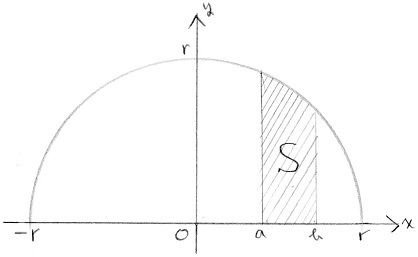
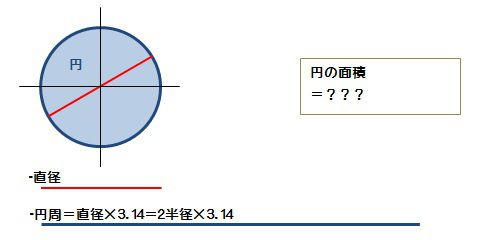
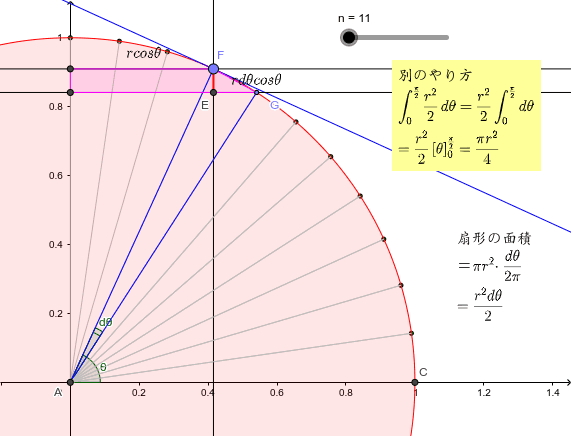
底面の円の直径方向に座標軸 をとり， の範囲で断面を求めて積分する． 底面の円に描いた黄色の直角三角形で，斜辺の長さは半径 に等しいから， 次に高さ は， のとき で傾きが の直線上にあるから， ここで は奇関数の積分だから0 は上半円の面積だから 円をぐるっと 1 回転することでドーナツの形になる。 これを 円環体 と言う。 考え方としては，大きな円から小さな円の面積を引くことでドーナツの面積を求め，それを積分で積み上げることで体積を求めます。 x=t x = t として，式を変形します。 t t の
円 面積 積分
円 面積 積分-円の面積の初等的な求め方は簡単だ。 でも、そこには積分の初期的な概念がある。 では、その初歩的な概念から積分へはどうやって至るのだろうか。 その積分を身体で感じるために、簡単に求まる円の面積を積分で求めてみよう。 ここから，楕円の面積公式の3通りの証明を紹介します。 グラフの拡大を用いる方法 愚直に定積分を計算する方法 ガウスグリーンの定理を使う方法 1は積分を知らなくても理解できますが，円の面積公式は認めてしまいます。残り2つは定積分を用いる方法
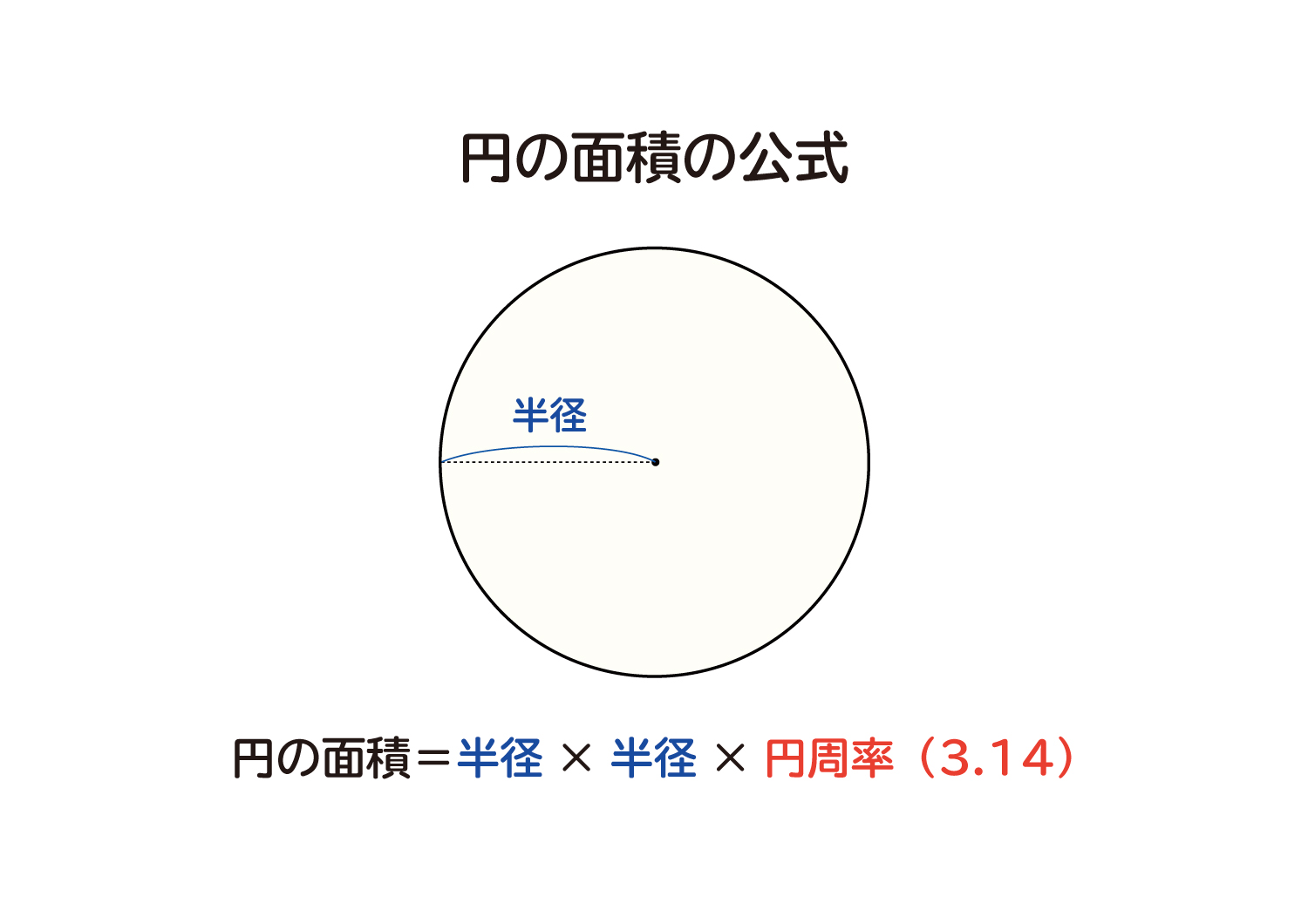
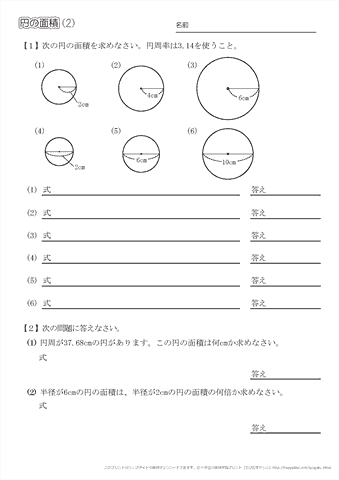
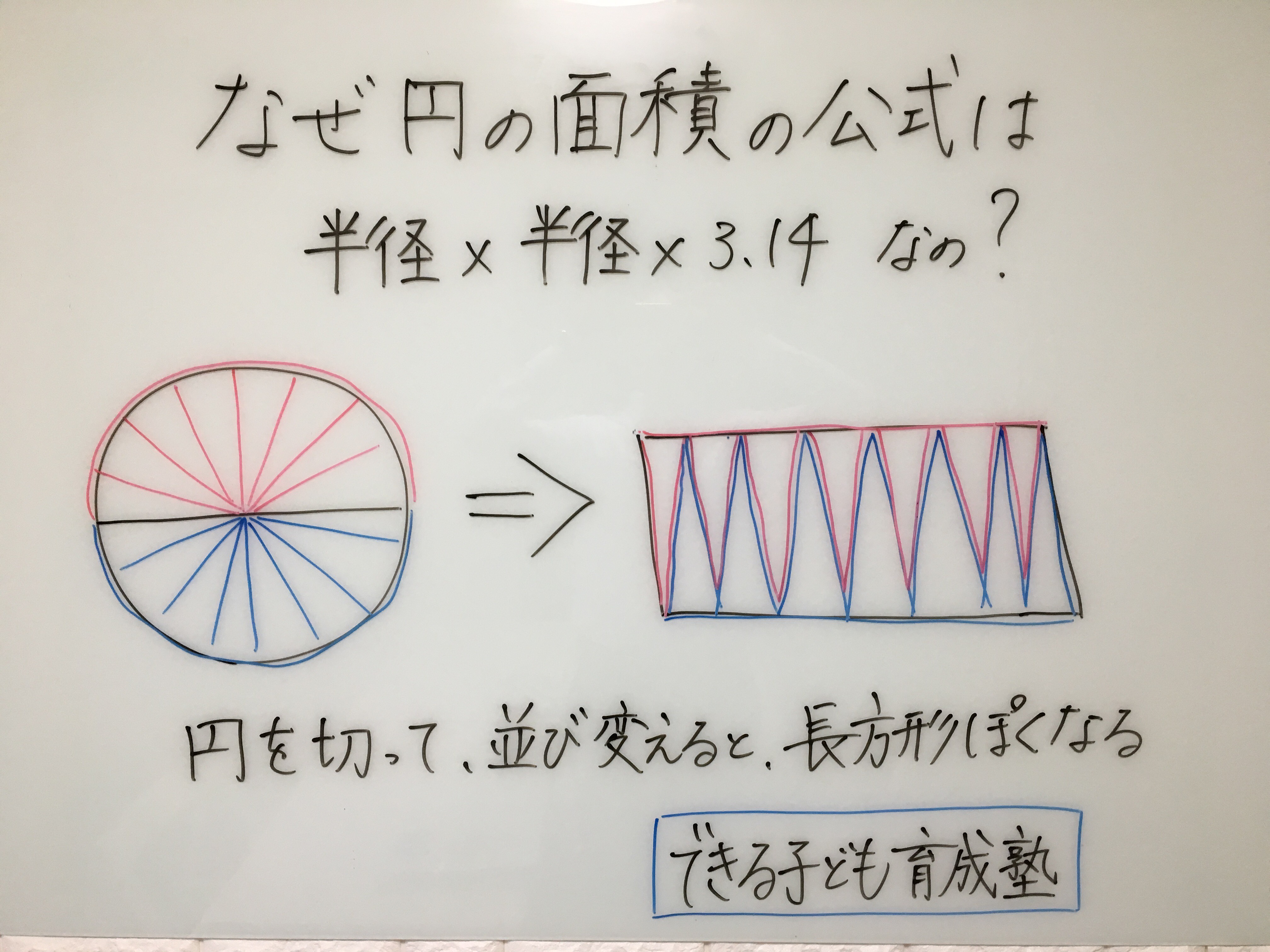
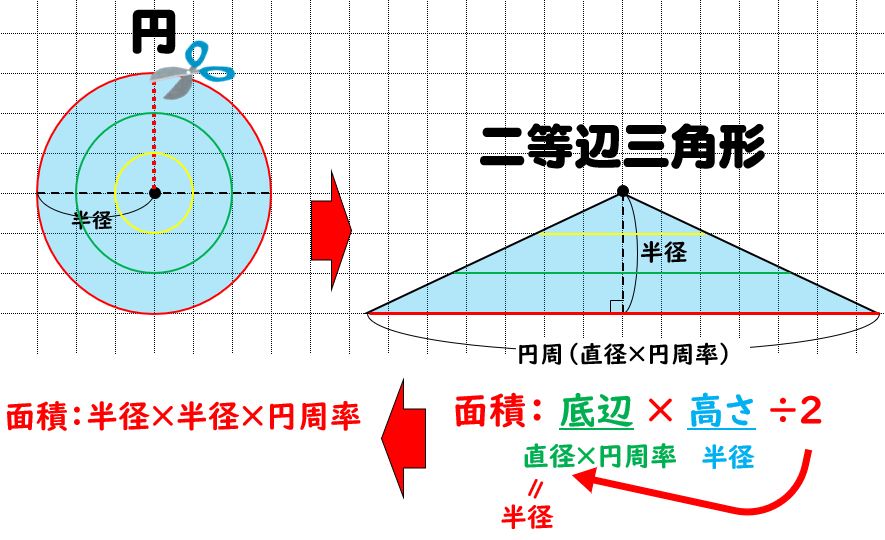
なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル
円の面積（ S urface area） π 円周率（= 314） r 円の半径（ r adius） 公式の導き方のイメージ この円の面積を求める公式は、円を無限個の扇形に分け、それを長方形につなぎ変えることで導くこと さらに、それぞれの円の扇形から三角形を引いたものを足せば赤色の面積が求められることが見えます。 図のように角度θ1、θ2を置くと、 s = ((円o1の角度θ1扇形の面積) (円o2の角度θ2扇形の面積) (三角形ao1o2の面積)) * 2 と求められます。 放物線を使った面積と不定積分 ここでは、 f (x) = x2 f ( x) = x 2 とします。 この不定積分は、 基本整式の不定積分 で見たように ∫ f (x)dx = ∫ x2dx = 1 3x3 C ∫ f ( x) d x = ∫ x 2 d x = 1 3 x 3 C となります（ C は積分定数）。 これは、「微分して f (x) = x2 f ( x
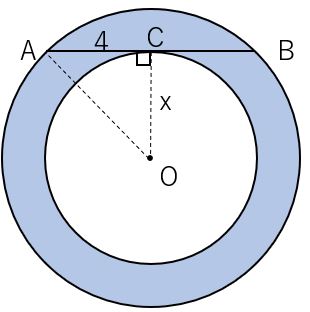
円の面積 複雑でよく間違える計算なので助かった。 食卓を買い替えるにあたり、丸ちゃぶ台サイズ90φか100φかかなり悩みました。 いっそ間をとって95φもありかなと思ったり。 ちなみに現テーブルは長方形90×60。 夫が現テーブルを手狭に感じている なので、 $0$ から $3$ まで積分するということは、この円の右上の部分である $\dfrac{1}{4}$ を表しているので、\ \frac{3^2}{4}\pi \となり、これを $\dfrac{8}{3}$ 倍して、楕円の面積が $6\pi$ とあることがわかります。積分 sinθ の図形による理解 ∫ sin θ d θ の積分を図形を用いて直感的に理解する． 左側の図は単位円，右側の図は y = sin θ のグラフである． 図において赤色の面積と青色の面積は等しい． ∫ 0 π 2 sin θ d θ = − cos θ 0 π 2 = − cos π 2 cos
円 面積 積分のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
 実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
 実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
「円 面積 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 実践記録算数５年 | 実践記録算数５年 |  実践記録算数５年 |
 実践記録算数５年 |  実践記録算数５年 | 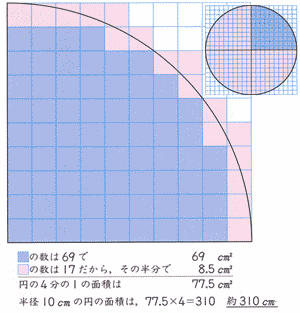 実践記録算数５年 |
 実践記録算数５年 | 実践記録算数５年 | 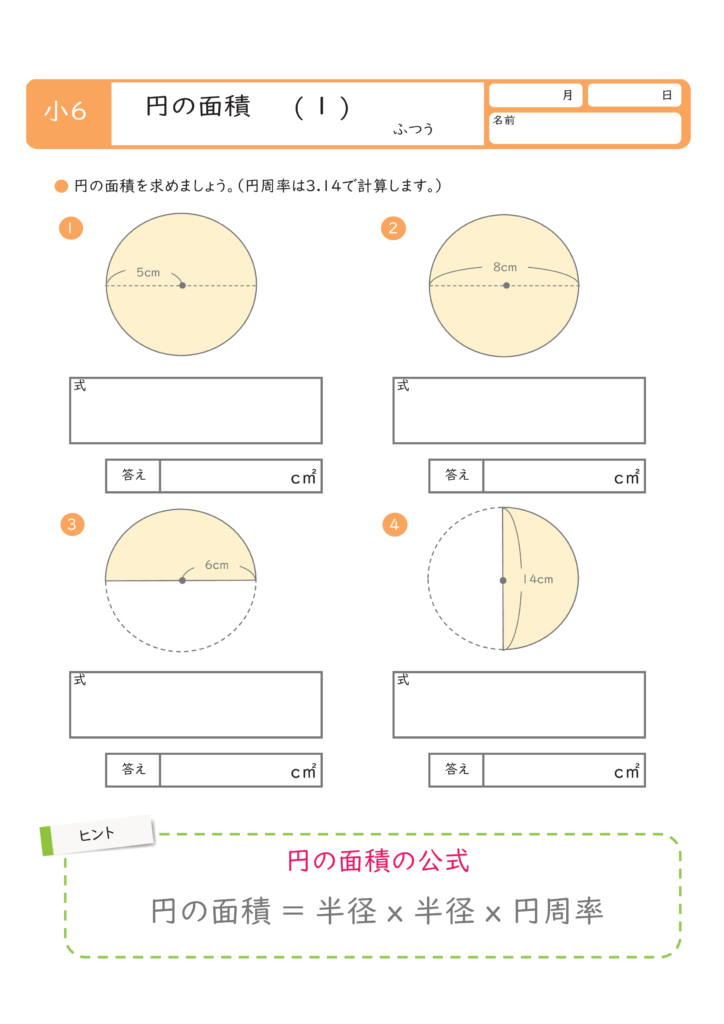 実践記録算数５年 |
「円 面積 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
実践記録算数５年 | 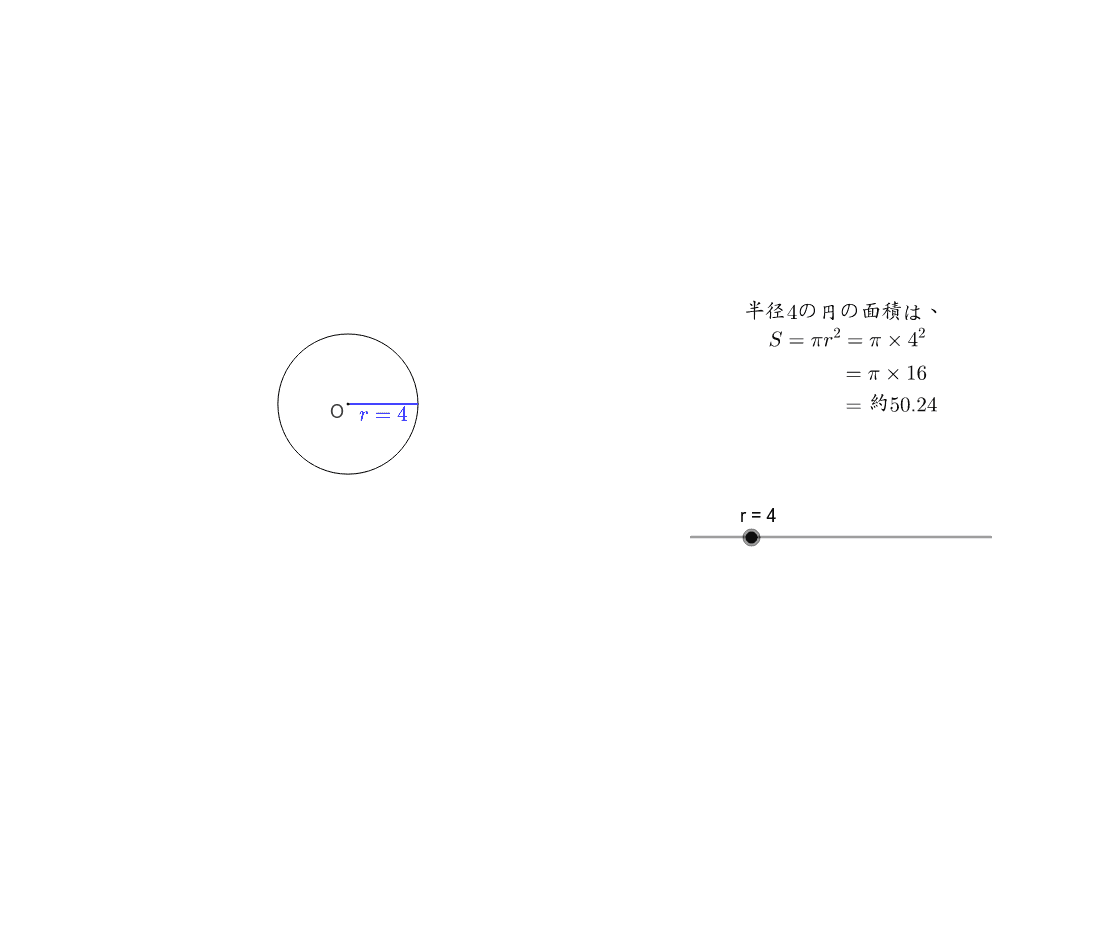 実践記録算数５年 | 実践記録算数５年 |
「円 面積 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 実践記録算数５年 | 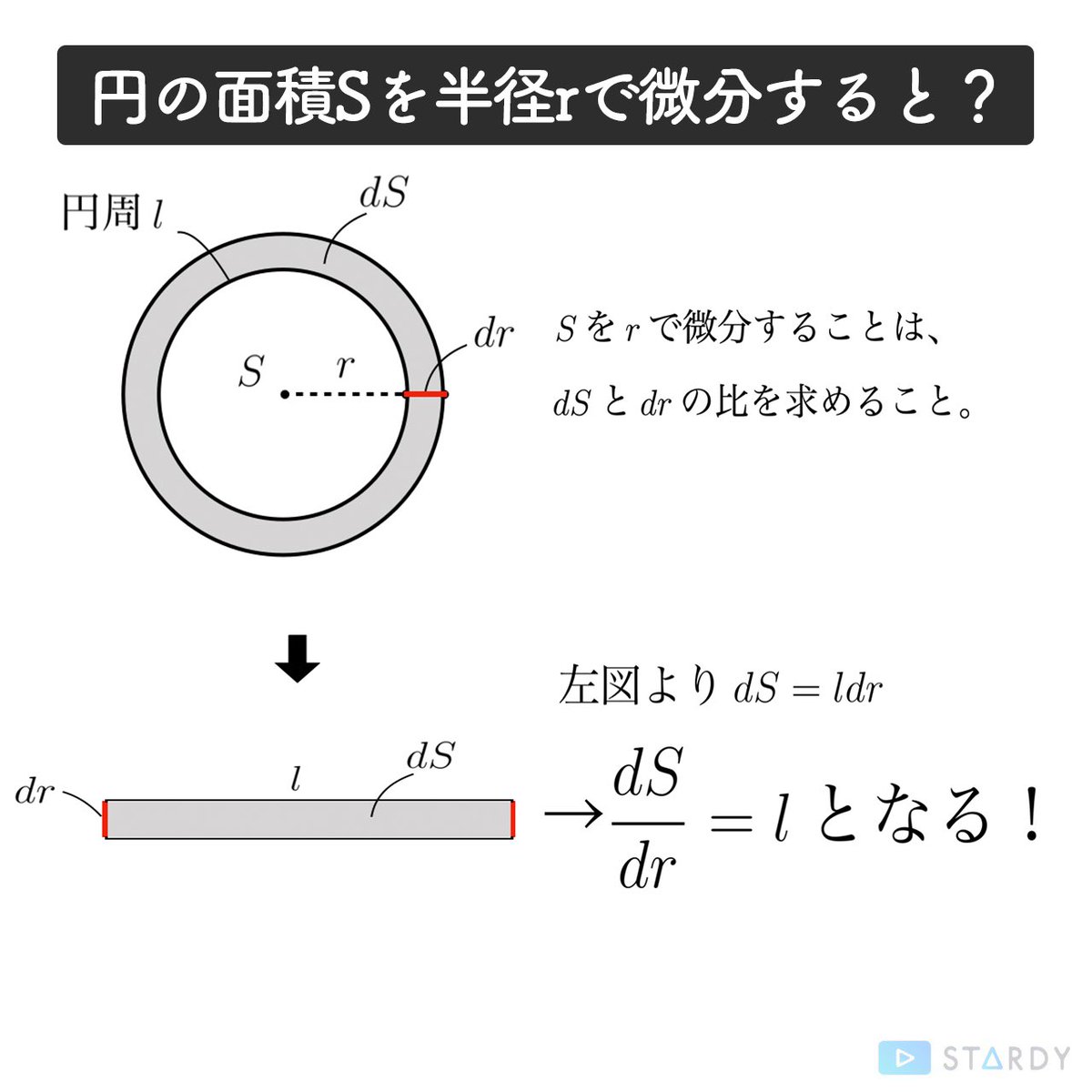 実践記録算数５年 |  実践記録算数５年 |
 実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
 実践記録算数５年 |  実践記録算数５年 | 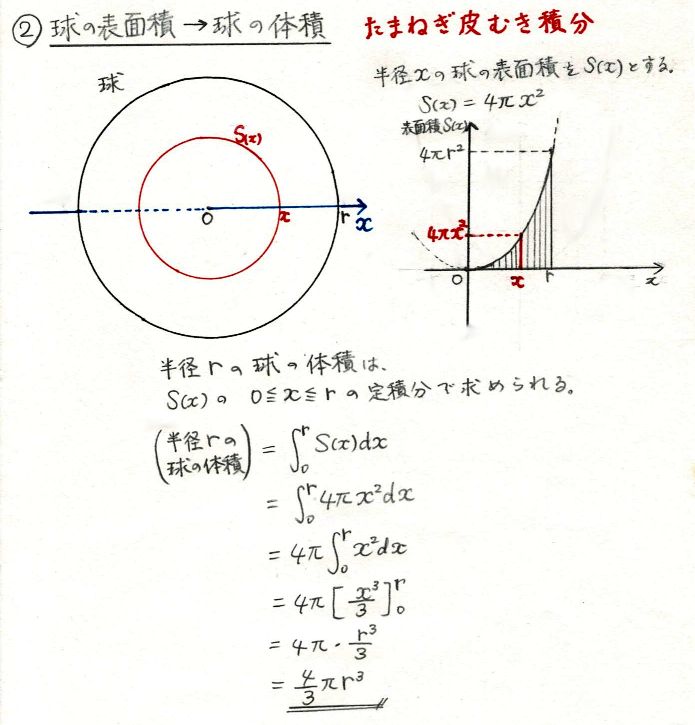 実践記録算数５年 |
「円 面積 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 実践記録算数５年 | 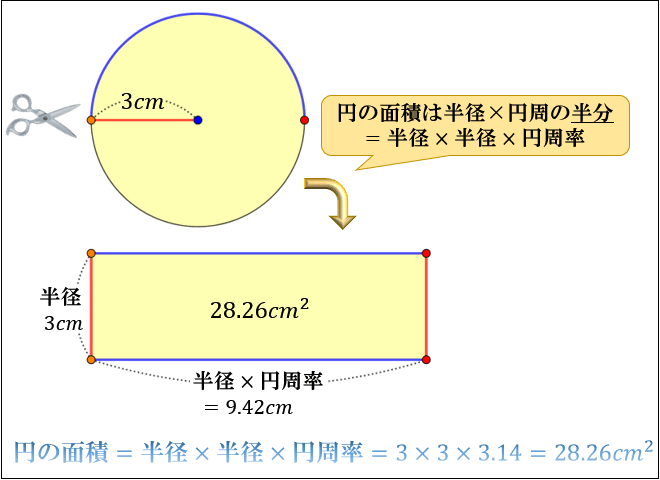 実践記録算数５年 |  実践記録算数５年 |
実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |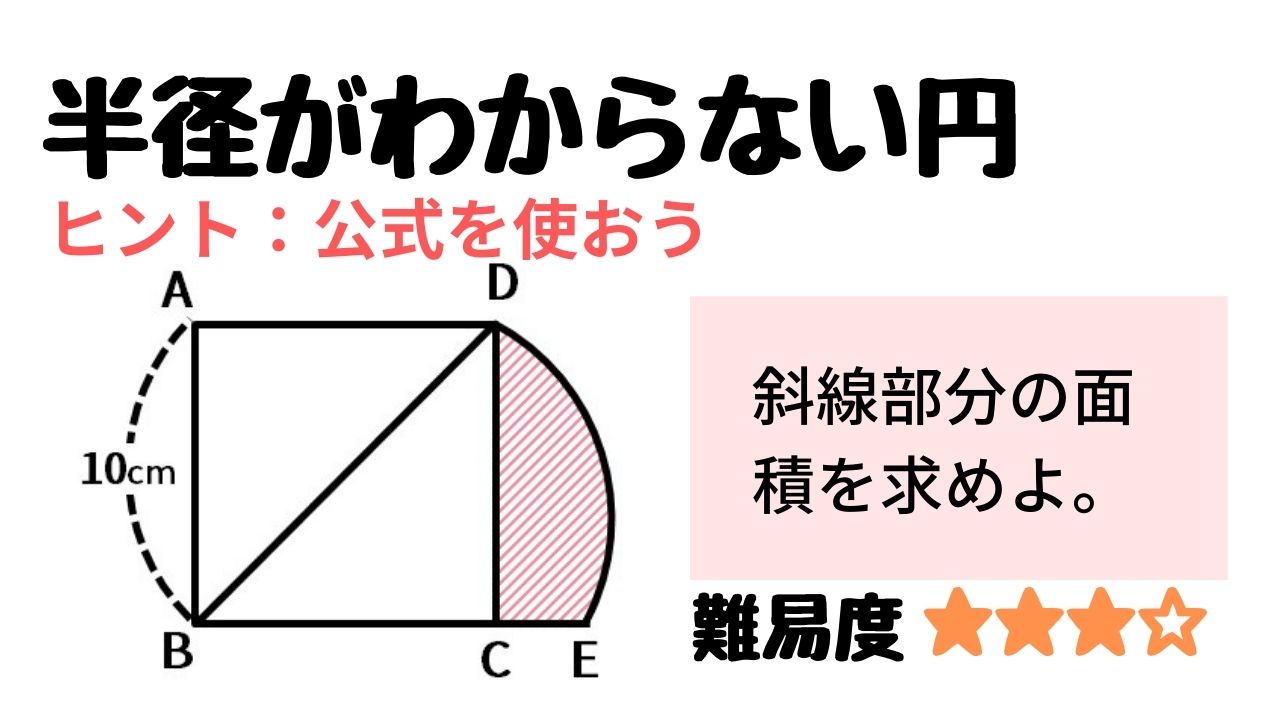
 実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
「円 面積 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 実践記録算数５年 | 実践記録算数５年 |  実践記録算数５年 |
 実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
「円 面積 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
 実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
 実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
「円 面積 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
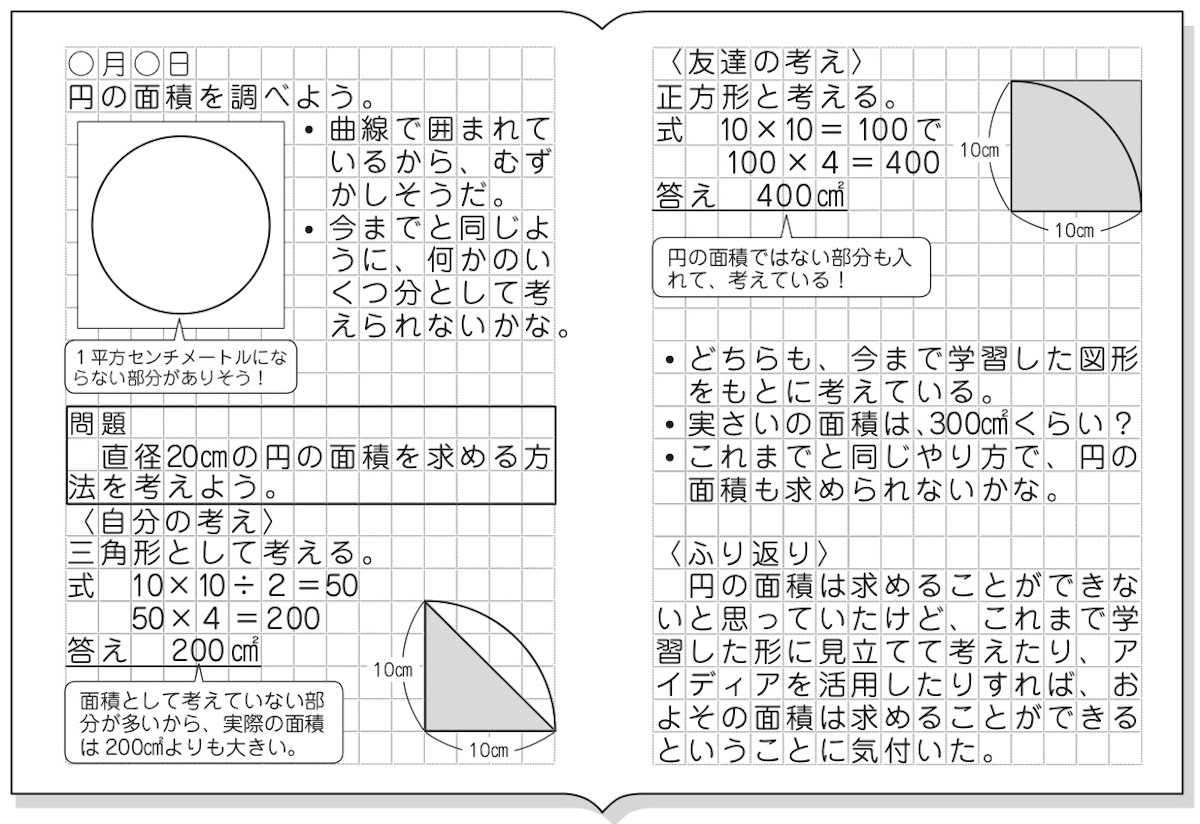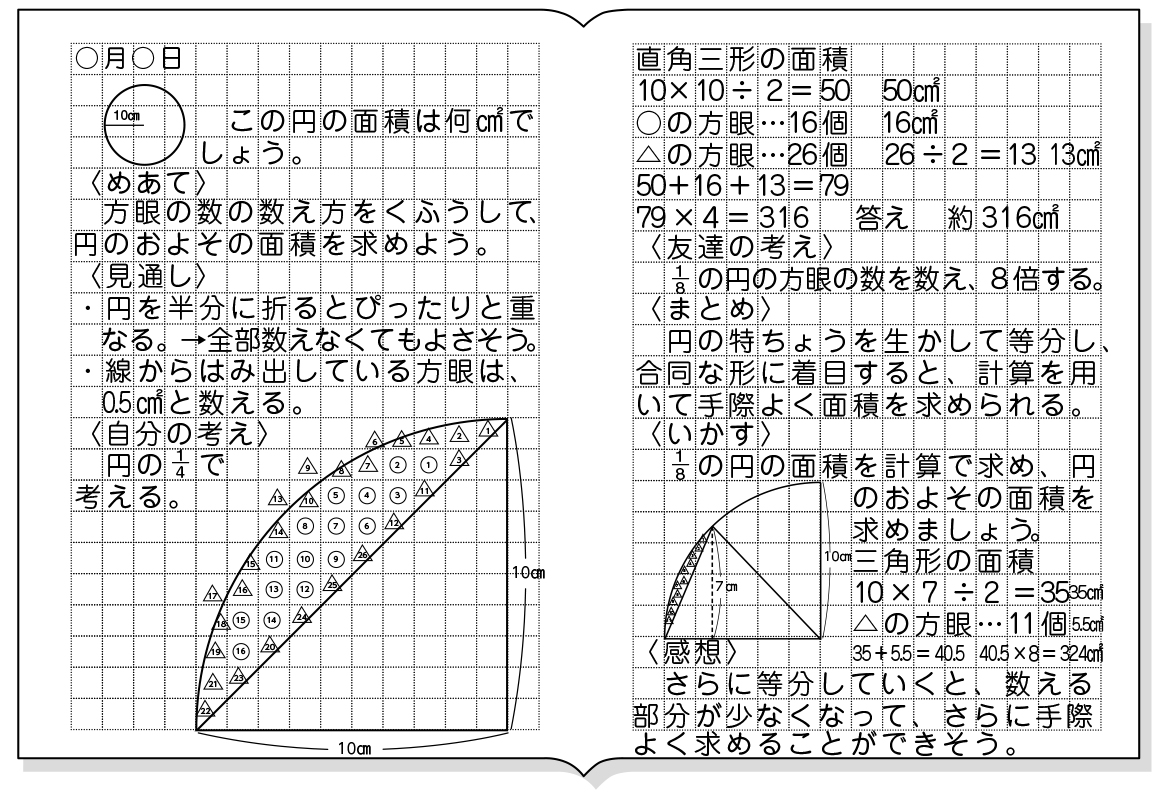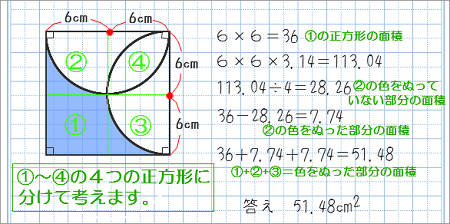 実践記録算数５年 | 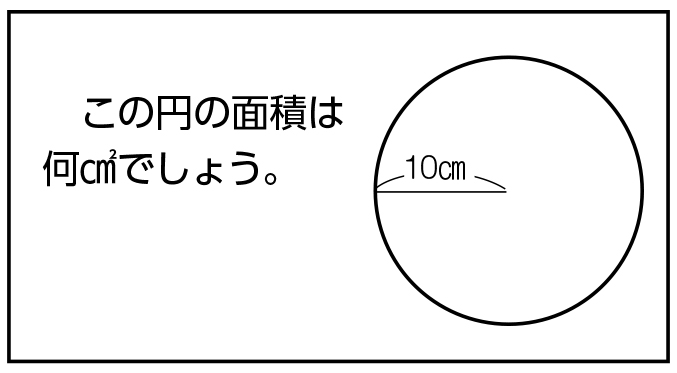 実践記録算数５年 |  実践記録算数５年 |
実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |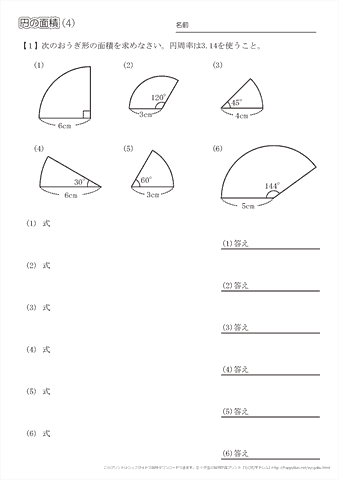
 実践記録算数５年 |  実践記録算数５年 | 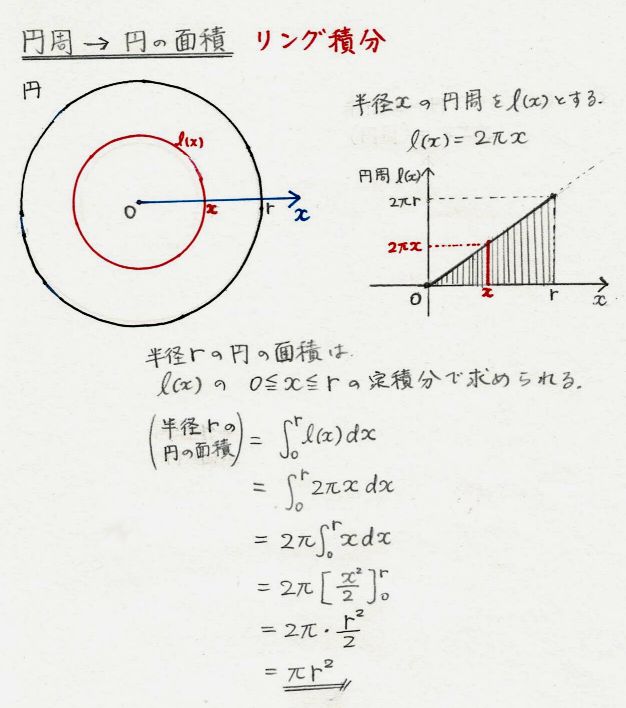 実践記録算数５年 |
「円 面積 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
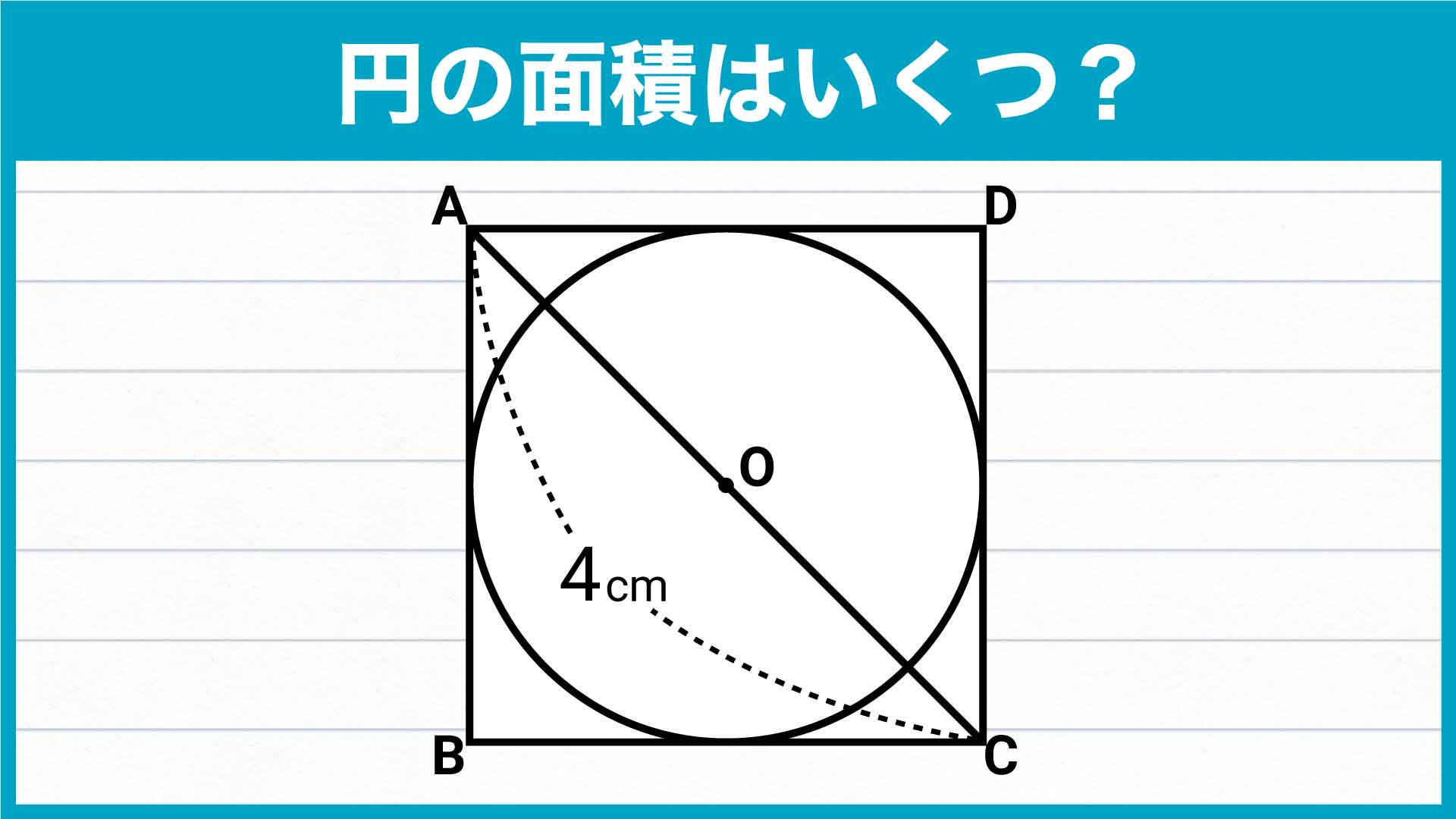 実践記録算数５年 | 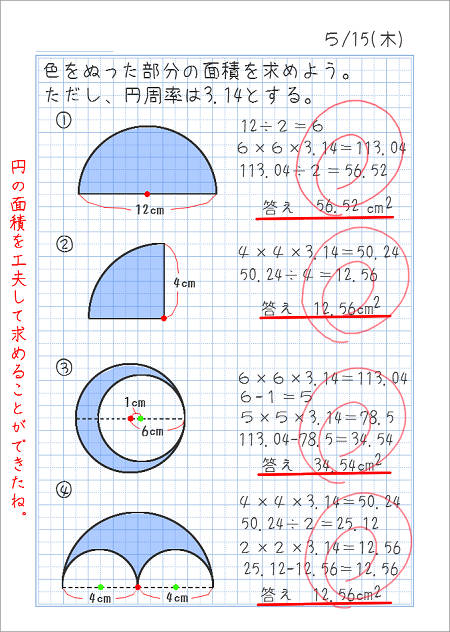 実践記録算数５年 |  実践記録算数５年 |
 実践記録算数５年 |  実践記録算数５年 | 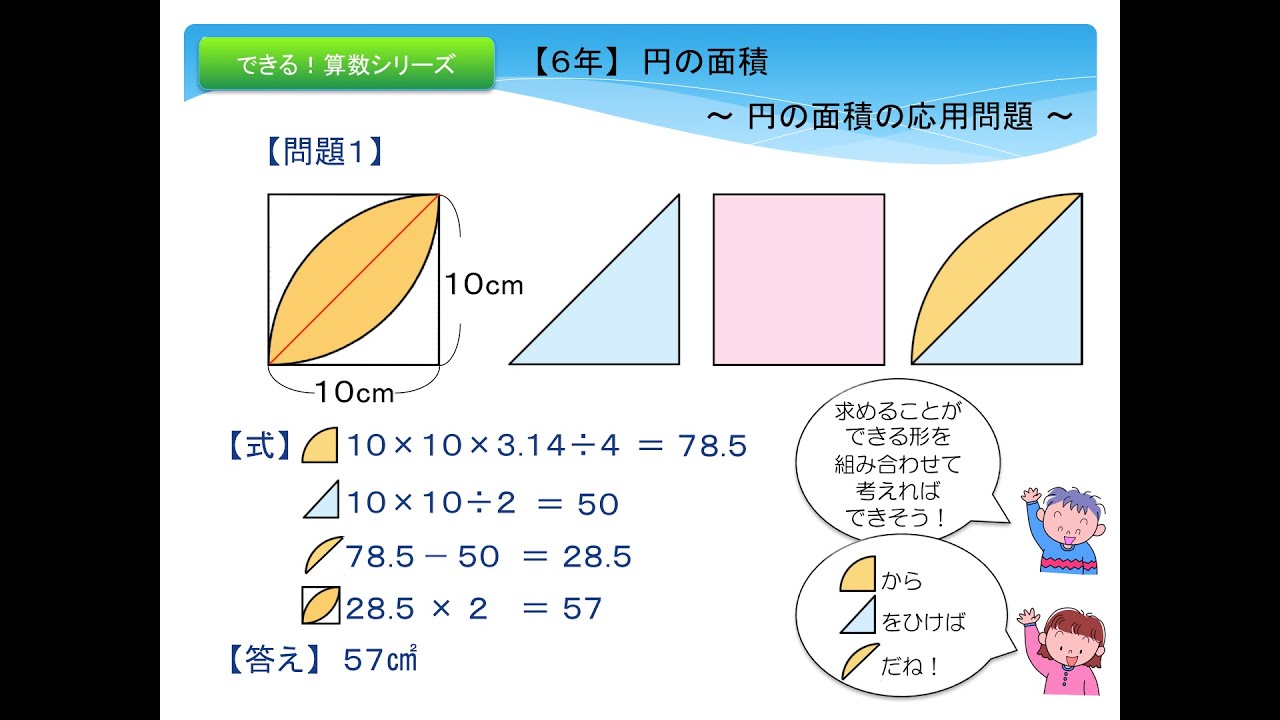 実践記録算数５年 |
 実践記録算数５年 | 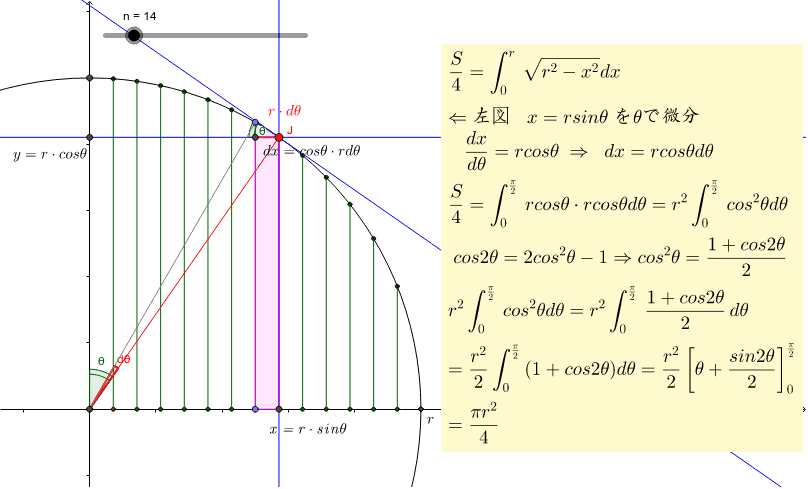 実践記録算数５年 | 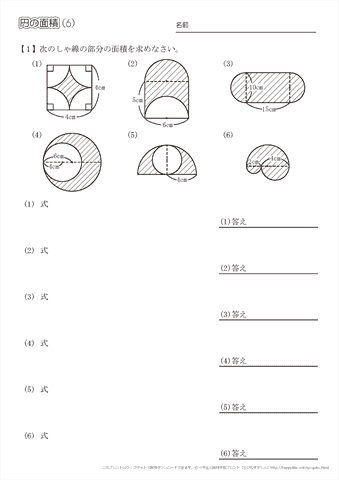 実践記録算数５年 |
「円 面積 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
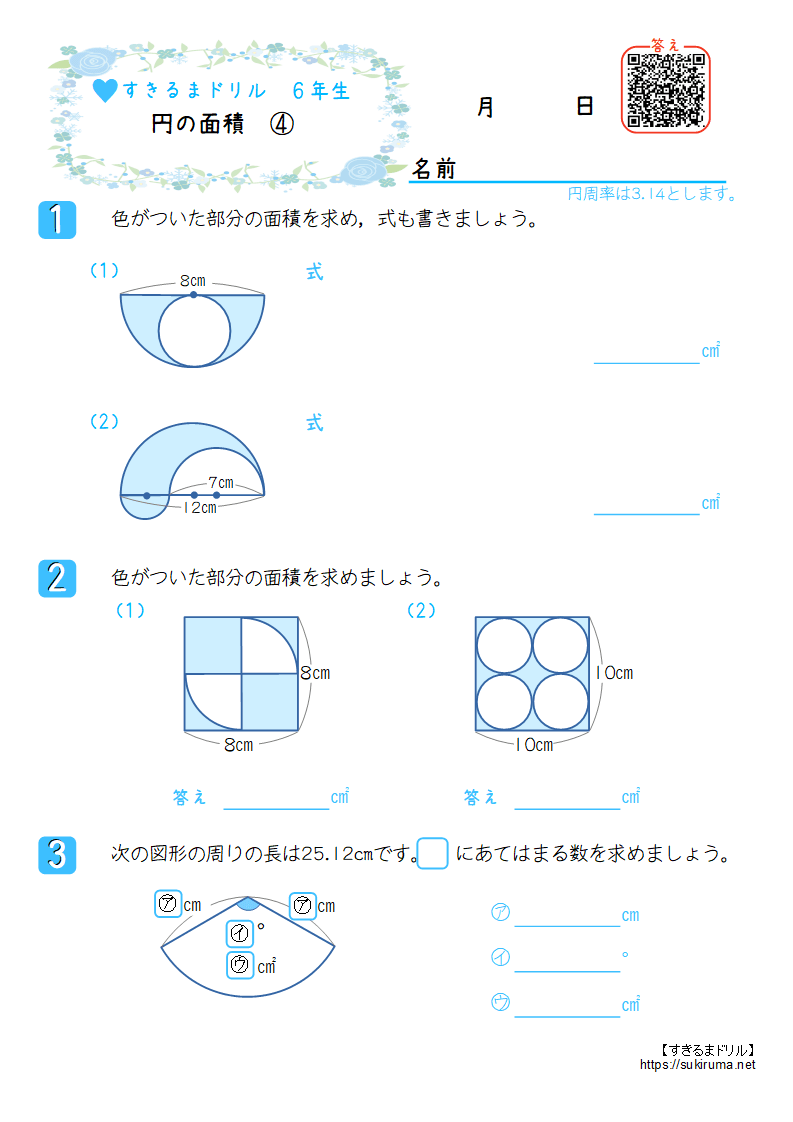 実践記録算数５年 | 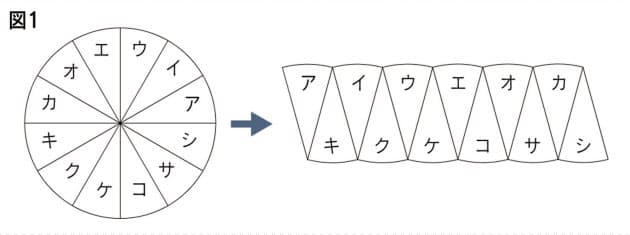 実践記録算数５年 | 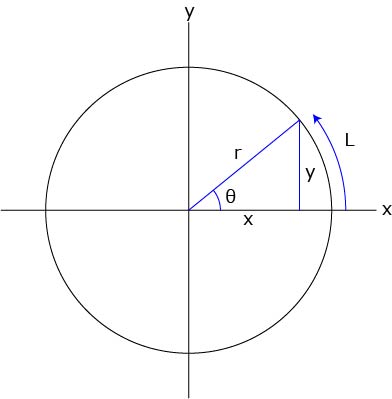 実践記録算数５年 |
 実践記録算数５年 | 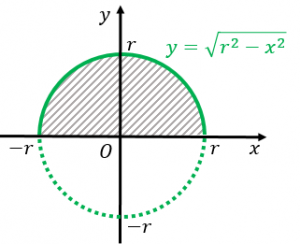 実践記録算数５年 | 実践記録算数５年 |
実践記録算数５年 | 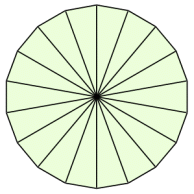 実践記録算数５年 |  実践記録算数５年 |
「円 面積 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
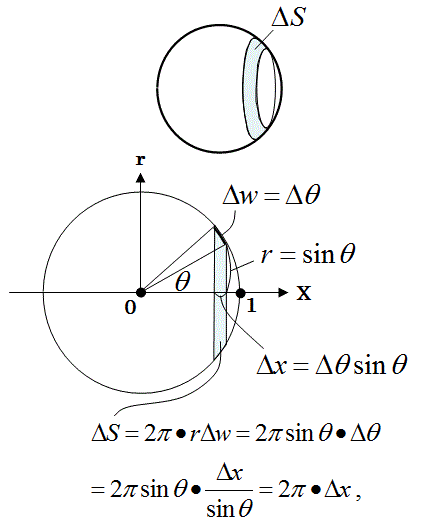 実践記録算数５年 | 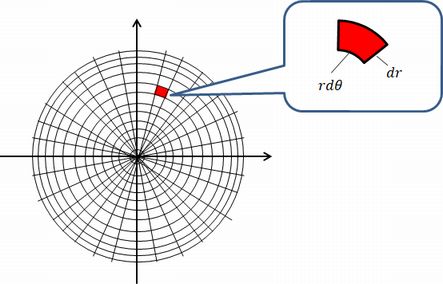 実践記録算数５年 |  実践記録算数５年 |
 実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
 実践記録算数５年 |  実践記録算数５年 | 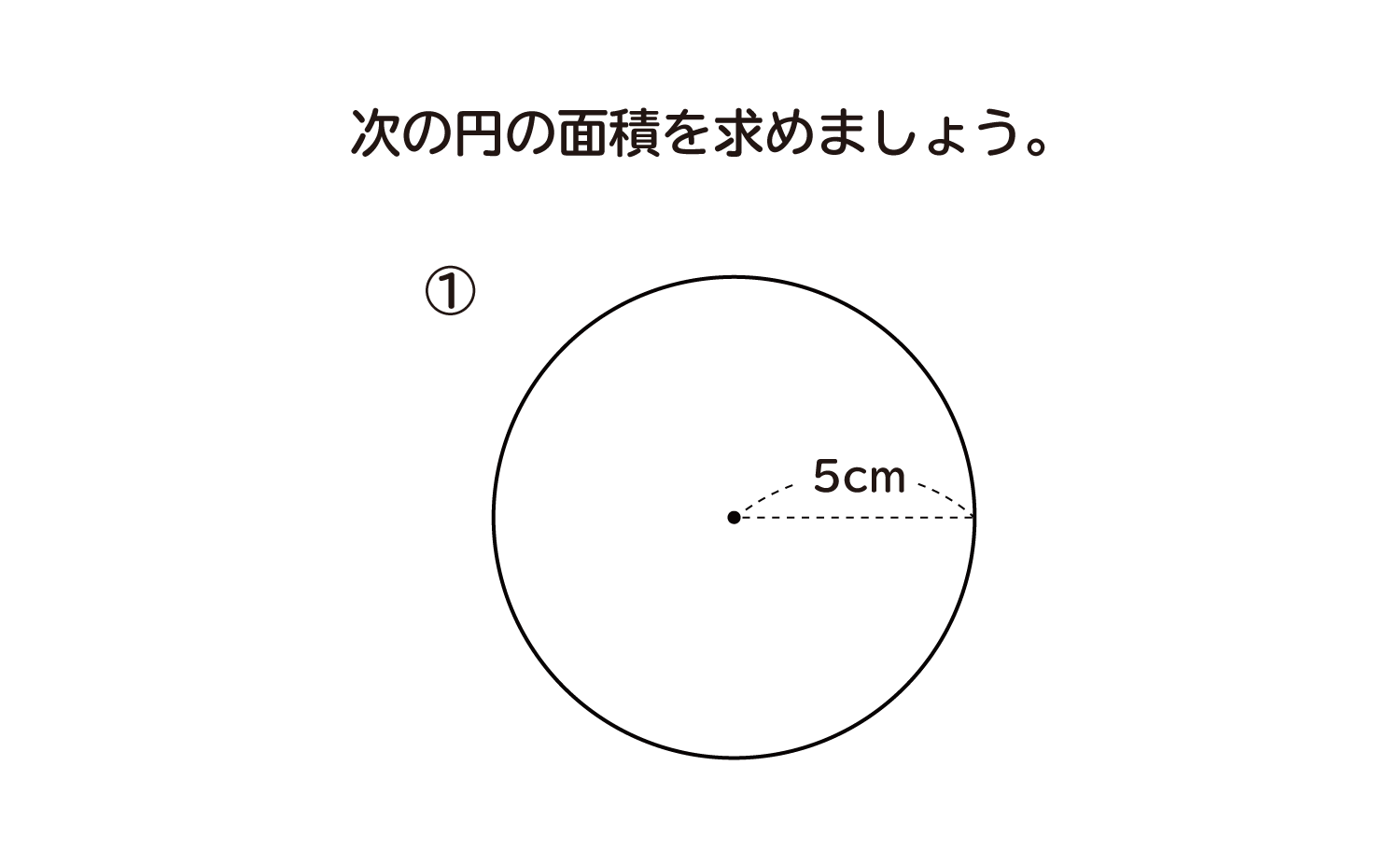 実践記録算数５年 |
「円 面積 積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 実践記録算数５年 |  実践記録算数５年 |  実践記録算数５年 |
 実践記録算数５年 |  実践記録算数５年 |
円を扇形に切って並べ直してみると 円の面積の公式はご存じの通り、πr 2 である。 πは円周率、rは半径だ。 ではなぜ、この式になるの 「微分・積分」の勉強 （1）積分： 以下の問題を考えます。 問題 半径 1 の円の面積Sをπと定義する。 面積S＝π この面積Sを求めよ。 （解答） この問題は、以下の様に解くことができます。 円を、以下の図の様な短冊に分割し、 その
0 件のコメント:
コメントを投稿