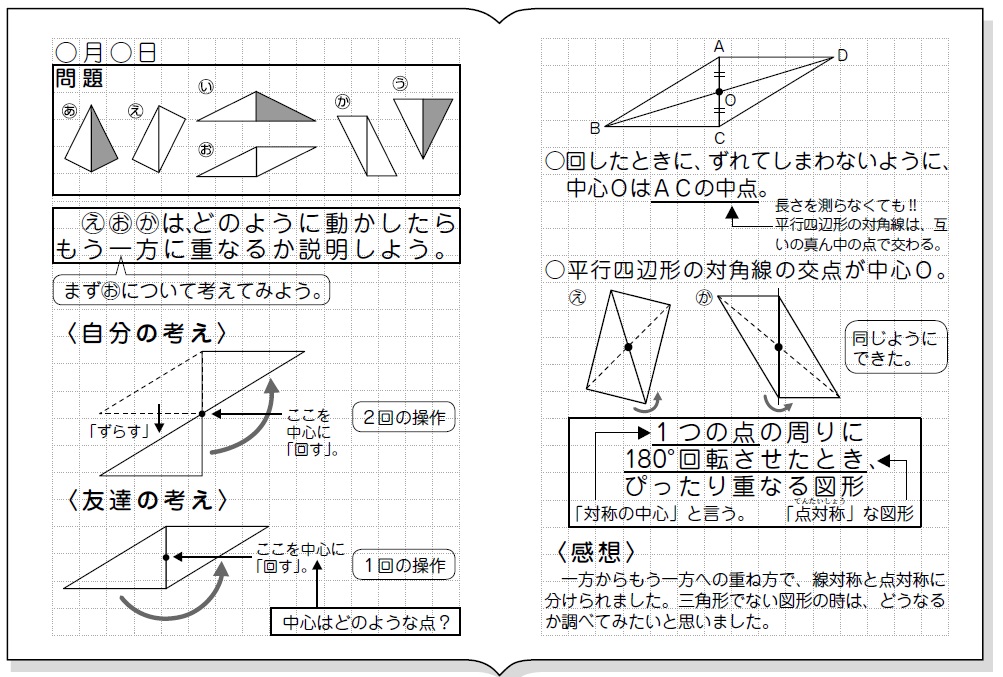
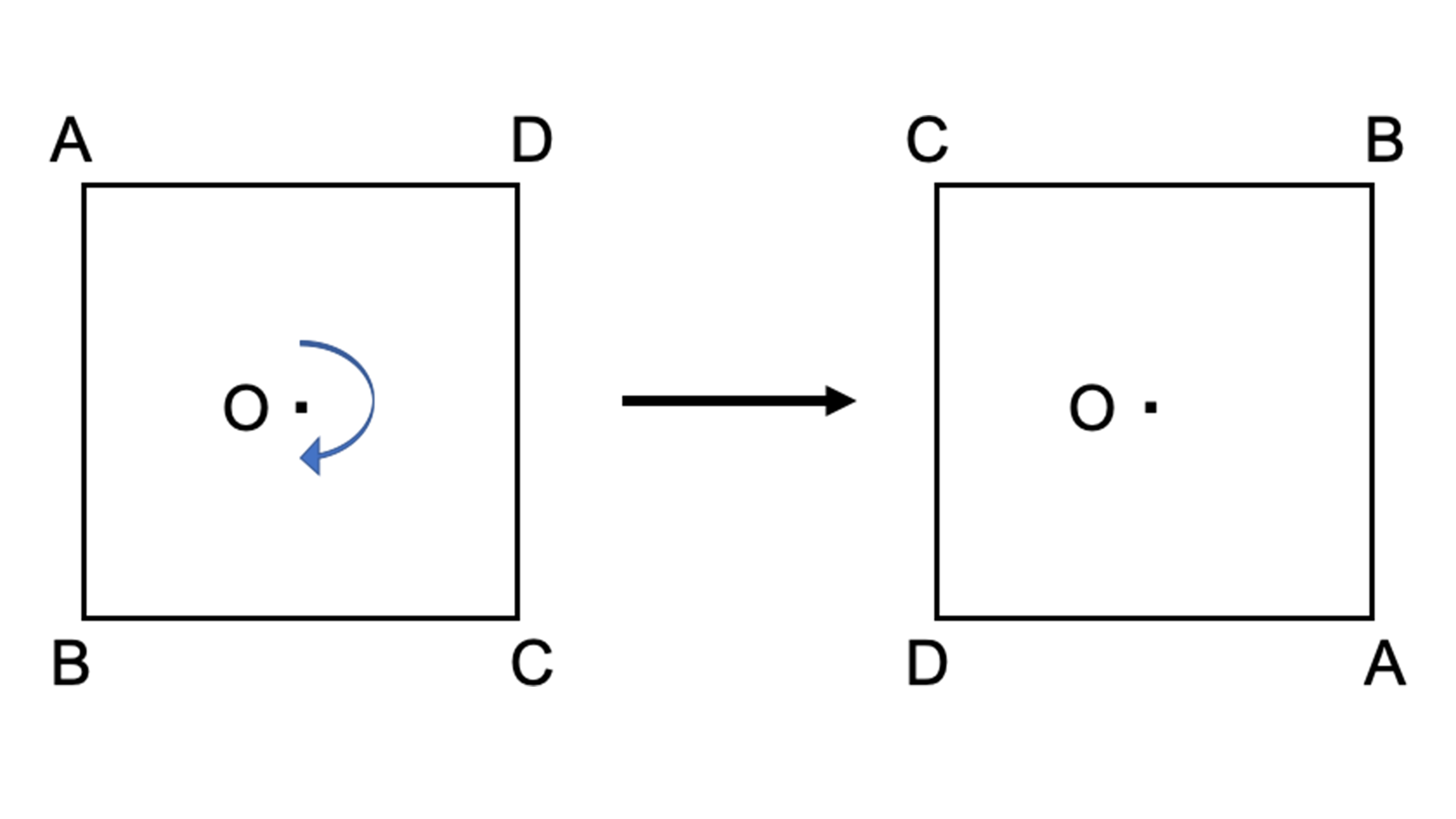
点対称かどうかを見分けるには・・・ 対応する点どうしを直線 で結んでみると対称の中 心が見えてくるよ 名前( ) 線対称対称の軸で2つに折ると の部分がぴったり重なる 点対称対称の点を中心に180 度回転 するともとの図形にぴったり重 なる算数 対称な図形③ 今日のめあて いろいろな図形について線対称か点対称かどうか調べて、それぞれの図形の特徴を考えよう 用意するもの 折り紙4枚(必要な人はvtrを見てもっと使ってもよいです) 1 動画を3:00で止めましょう 線対称な図形とは 半分におると重なり へん、点、角度全てに 対応する物がある この事を利用したら かけます! ま、重なれば線対称ということ! ちなみに線対称、点対称 終わったら文字式をやるらしいよ~ みんとさん(埼玉・11さい)からの答え

楽天ブックス 考える力を育てる 天才ドリル 平面図形が得意になる点描写 線対称 小学校全学年用 算数 認知工学 本
点対称な図形 折り紙
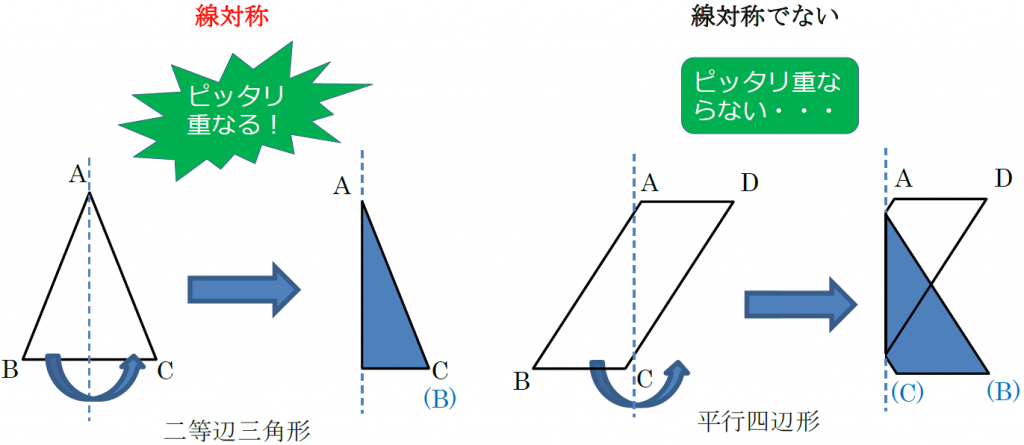
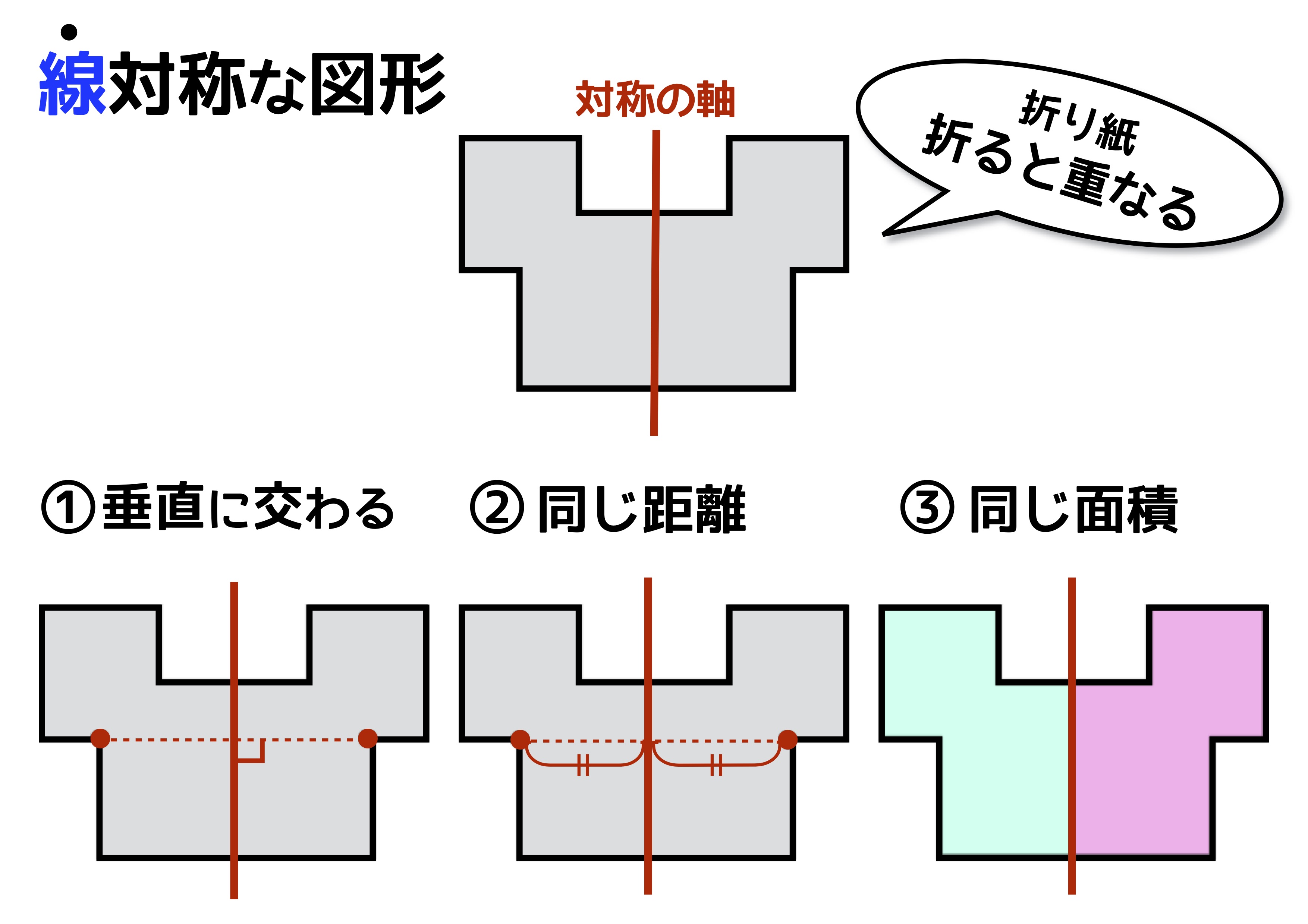
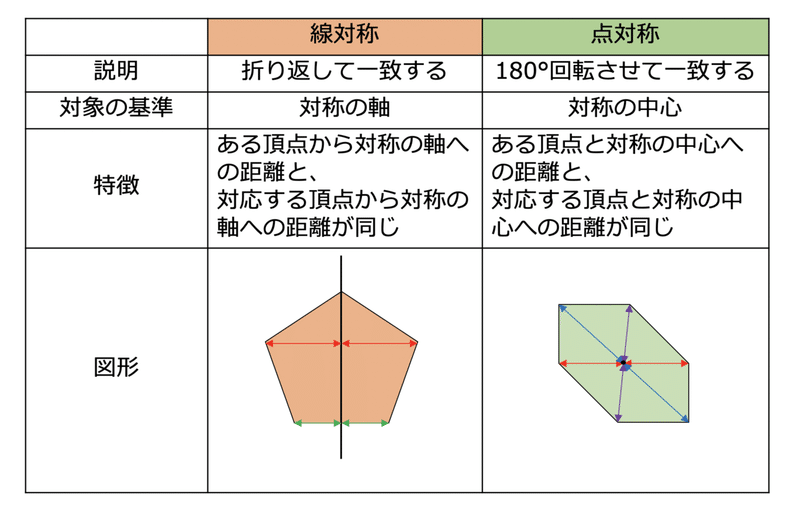
点対称な図形 折り紙-線対称、点対称な図形の性質を理解することができる。 (知識・理解) 対称 線対称 能生中学校 点対称 いろいろな図形と 対称 折り紙を折ったり、切ったりして 二等辺三角形やひし形をつくる。 折り紙を何回か折り、それを切り抜線対称: 「対称の軸」で折り曲げると図形がピッタリ重なる、対称の軸が存在する。 点対称: 「対称の中心」で180°回転させたら元の図形と重なる、対称の中心が存在する。



Http Cms Nerima Tky Ed Jp Weblog Files 103 Doc Pdf
(10点×1問) 線対称な図形を対称の軸で切ると、 な2つの形ができる。 5 下の地図記号は郵便局のマークで、線対称な図形です。対称の軸をかき入れ、 にあてはまる言葉を書きましょう。(10点×2問) う、お 直線kl 点 f 辺 ih 垂直 合 ①対称の軸は、どれです 図形:折り紙の線対称(成蹊小学校) 左のお部屋の折り紙を、線のところで切って穴を空け、開くとどんな形ができるか、右の4つの形の中から選んで をつける。 形が回っていることもあ│┌─┘ └┘ ・点対称な図形は、面積を半分にする線が無限にあるのか ・点対称な図形を書いてみよう ・折り紙を使って、美しい模様を切り抜こう 四つ折りの折り紙に切り込みを入れて、広げるとどんな形になるかクイズ ・パソコンを使って、線対称
33 目 標 (1) 線対称や点対称の図形の美しさに関心をもち,線対称や点対称という観点から様々な図形を 考察する活動に意欲的に取り組み,自分なりの「問い」を連続・発展させていこうとすること対称④ (点対称な図形) 6年4月(p14〜16)前4 組 番名前 1 対称(点 てん 対 たい 称 しょう な図形) ア コ エ ケ ク キ イ ウ オ カ 1 左のような形について考えましょう。 ① 左の図は,点 てん 対 たい 称 しょう な図形です。対称の中心を見つけて,たとえば,折り紙を2つに折ったとき,折り目の両側がびったりと重なるので,その折り紙は線対称であるといえます。 線対称な図形では,対称の軸で折ったとき,重なり合う点,辺,角をそれぞれ 対応する点,対応する辺,対応する角 といいます。
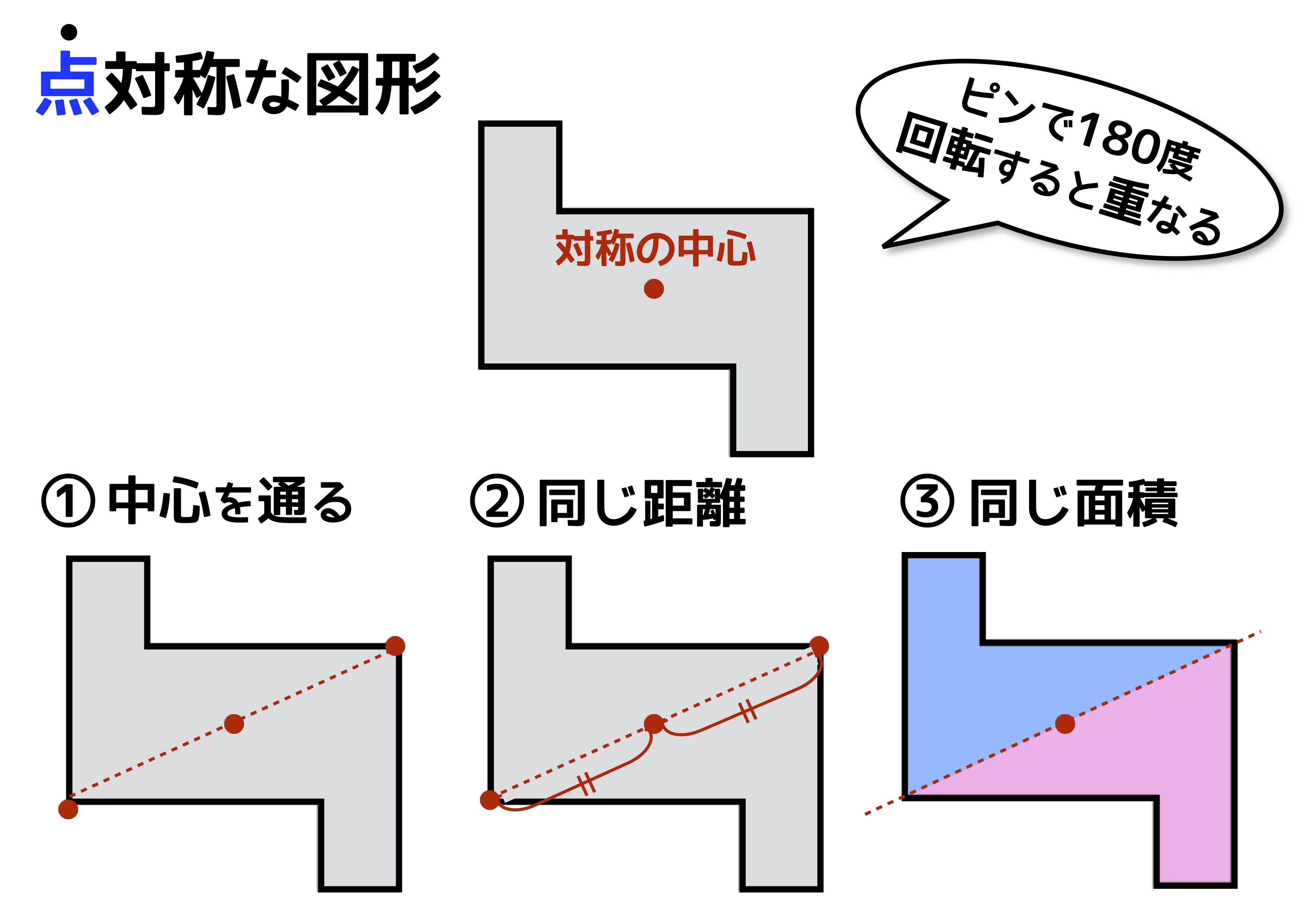
・線対称な図形を作図することができる。(技) 2 回転すると重なる形(p8~10) 3時間 5;② 線対称にも点対称にもなっており,対称の軸の数が8本の正多角形 4 ② 下の点対称な図形に対称の中心を かき入れましょう。 (かいた線は残しておきましょう。) 5 ② 点oが対称の中心になるように, 点対称な図形をかきましょう。 こちらも、点対称の図形の性質を使えば、正しく作図できます。 では、点対称な図形の性質とは何か? ①対応する辺の長さは等しい。 ②対応する角の大きさは等しい。 ③対応する点を結んだ線分は、対称の中心を通る。



Http Syou Oita Ed Jp Hita Kangi Files 62bde7776f21e44d32b0d4aca Pdf



Cms1 Ishikawa C Ed Jp Wakure Wysiwyg File Download 1 433
Amazonで山口 榮一のおりがみで学ぶ図形パズル 小学校全学年用 算数。アマゾンならポイント還元本が多数。山口 榮一作品ほか、お急ぎ便対象商品は当日お届けも可能。またおりがみで学ぶ図形パズル 小学校全学年用 算数もアマゾン配送商品なら通常配送無料。(3)線対称の考えで作った模様が点対称になっていることもあり、図形のもつ不思議な性質や 数学の美しさにふれる。 4 学習計画(全4時間) 4時間で学習させる。1時間目と3時間日の初め、4時間目の班発表は、一斉学習の形態で取 り組ませる。第1時で点対称、線対称の意味について学習した後、右図のような模様をつくり、さいころを振って陣取りをする。 さいころの目が偶数なら線対称、奇数なら点対称の図形をつくる。 2人組でそれぞれが最初の場所を決める。 (直角三角形のカードを置く)



1




線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ
この図形は、点対称な図形といえるかな? いえる いえない 折り紙を切ったり、はりつけたりして、線対称な図形や点対称な図形 を作ってみましょう。 ※合同な図形を2つ作ると、線対称な 図形や点対称な図形をつくること ができるよ!点対称な図形の書き方その1 中心点や対応する点や線に気づかせます。また、定規やコンパスの使い方を聞かれた時は教えます。 点対称図形の書き方 対称の中心が図形の辺にある場合 ↓ 動画作成協力・・動くイラストフリー素材 点対称な図形の書き方その2 今回は対称図形の問題です。 この問題を解くときは、折り紙を使って図形を正しく把握できるようにしておきましょう。 対称図形を解く時に必要となってくるのは、見えていない部分を頭の中で認識するための推理力です。 そして、2つ折りの時はできたけど、4つ折りになるとできなく



小6算数 対称な図形 指導アイデア みんなの教育技術



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ
そして折り紙自体が問題になっていなくても、回転体、点対称、線対称、角度といった単元は、やはり 折り紙を知っている子は図形の強い 傾向にあります。 オンライン教室で折り紙を用いた指導をしたため、その時の様子をお話しましょう。中学1年の平面図形の実践です。 できるだけ実際にさわったり作ったりするようにしました。 特に折り紙を利用しました。 図形の移動 対称移動(線対称) 回転移動 180度回転(点対称) 360度÷2 1度回転 360度÷3 90度回転 360度÷4点対称な図形を調べる。 点対称の意味を知る。 ・点対称の意味を理解している。(知) 6 点対称な図形の性



Math 点対称な図形のかき方 働きアリ



Www Nipec Nein Ed Jp Sc Risuu H21 H21suugaku 6mizuno Pdf
(7)「点対称な図形」をかいてみよう(5/19) ①P18問題点対称な図形をかきましょう。 ②①の図がどんな形になるか予想をノートにかきましょう。 ③めあて点対称な図形の性質を使った、点対称な図形の書き方を考えよう。③折り紙の「切り開き」による線対称の理解の学習に使用する。 折り紙を「2つ折り」あるいは「4つ折り」にして、 その1部を切って開くことで、線対称な図形の理解を進めることができます。 ペーパー学習だけでなく、 このようにしてできた形は「線対称な図形」になります。 ④鏡を使った図形パズル 年長さんでは、模様がかかれた立方体のブロック2個を鏡に映し、付属の見本カードと同じ模様をつくる図形パズルを用いて線対称な図形に親しみます。




6年生のみなさんへ 堀津小blog 羽島市立堀津小学校



私の実践 私の工夫 算数 児童が楽しみながら目をキラキラと輝かせて取り組む授業を目指して 6年 対称な図形 啓林館
点対称な図形を作図する。 知 点対称な図形の性質を用い て,点対称な図形を作図す ることができる。 主 線対称な図形を,性質をもと に作図したことを振り返り, 点対称な図形も性質をもと に作図しようとしている。 4 多角形と対称 ( 教p~21) 8線対称の利用として、折り紙を使って線対称の理解を深める。 2回折った直角三角形 問題づくり 第5時 点対称の性質について理解し、点対称の図形を作図する。点対称な図形(平行四辺形)と線対称な図形(二等辺 三角形)の2つの図形に折った折り紙を用いて(写真1), 乳幼児がどのように形構成していくのか,展開の特徴を 観察調査し,パターンの分類を行った。 表1 連想内容の分類と定義 カテゴリ 定義 例
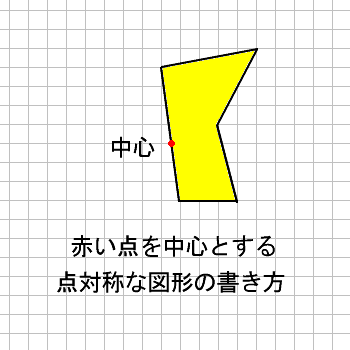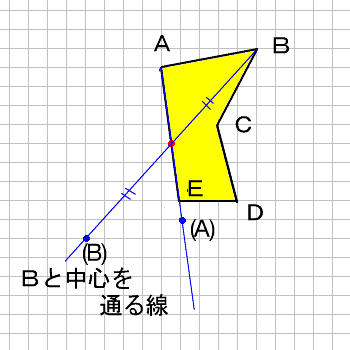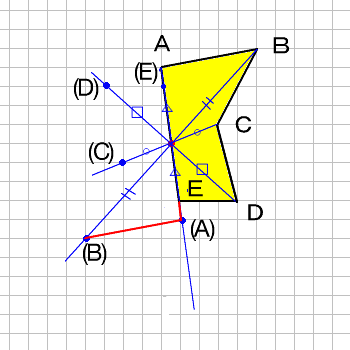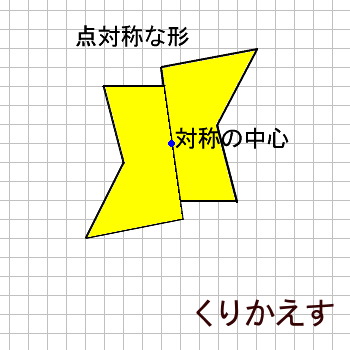



6年算数線対称点対称図形 わかる教え方




折り紙で線対称
折り紙でひらめく補助線の幾何 加藤 渾一(北海道岩見沢西高等学校) 第56回数学教育実践研究会 06年1月28日 於:ニッセイMK折り紙を図形(幾何)教育に活用する利点は,次の5 点であると考えられる注1)。第一に,道具は紙のみであ 第一に,道具は紙のみであ り,いつでも・どこでも・手軽に使用することができること,第二に,折り紙で図形(線・角・多角形・多面体線対称な図形を作成することになる。「線対称・点対称」な図形は、中学校「数学」第一学 年で習う。 ③ 一般に、3 等分は難しいが、2 等分は優しい。ギリシャ作図問題 (定規とコンパスによ る角の 3 等分問題) からも自然な帰結と思われる。 ④ 折り紙を
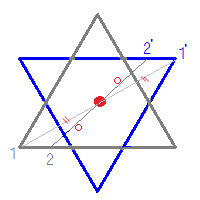



線対称 点対称
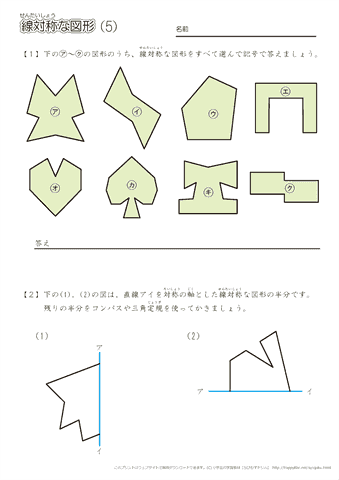



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生
合同な図形の性質をもとにして対称な図形について観察し、図形の見方を豊かにする。 展開 学習活動・留意点 既習事項・支援・評価 課 題 把 握 自 力 解 決 発 表 検 討 T アルファベットをABCの順で言い線対称・点対称、図形が線対称、 点対称である かを判断し、説 明することが できる。 合同の意味を理 解している。 観察評価 記録カード 3 4 対称な図形の性質 線対称、点対称な 図形の性質を調 べようとしてい る。 平面図形に関 する用語や記 号を理解7 1 め 色々な四角形が線対称な図形か点 対称の図形か調べよう。 、p457の問題と教科書に書かれ ている表をノートに書く。 ・台形、平行四辺形、ひし形、長 方形、正方形を調べ、表に答え 教科書 授業用 ノート ~先生からのお願い~ 点対称の図形を書くの



6年算数 線対称な図形の理解は折り紙から 高岡市立国吉義務教育学校



6年算数線対称点対称図形 わかる教え方



Www Edu City Yokohama Jp Sch Kenkyu Es Sansu Pdf Jirei Jirei Pdf




楽天ブックス 考える力を育てる 天才ドリル 平面図形が得意になる点描写 線対称 小学校全学年用 算数 認知工学 本
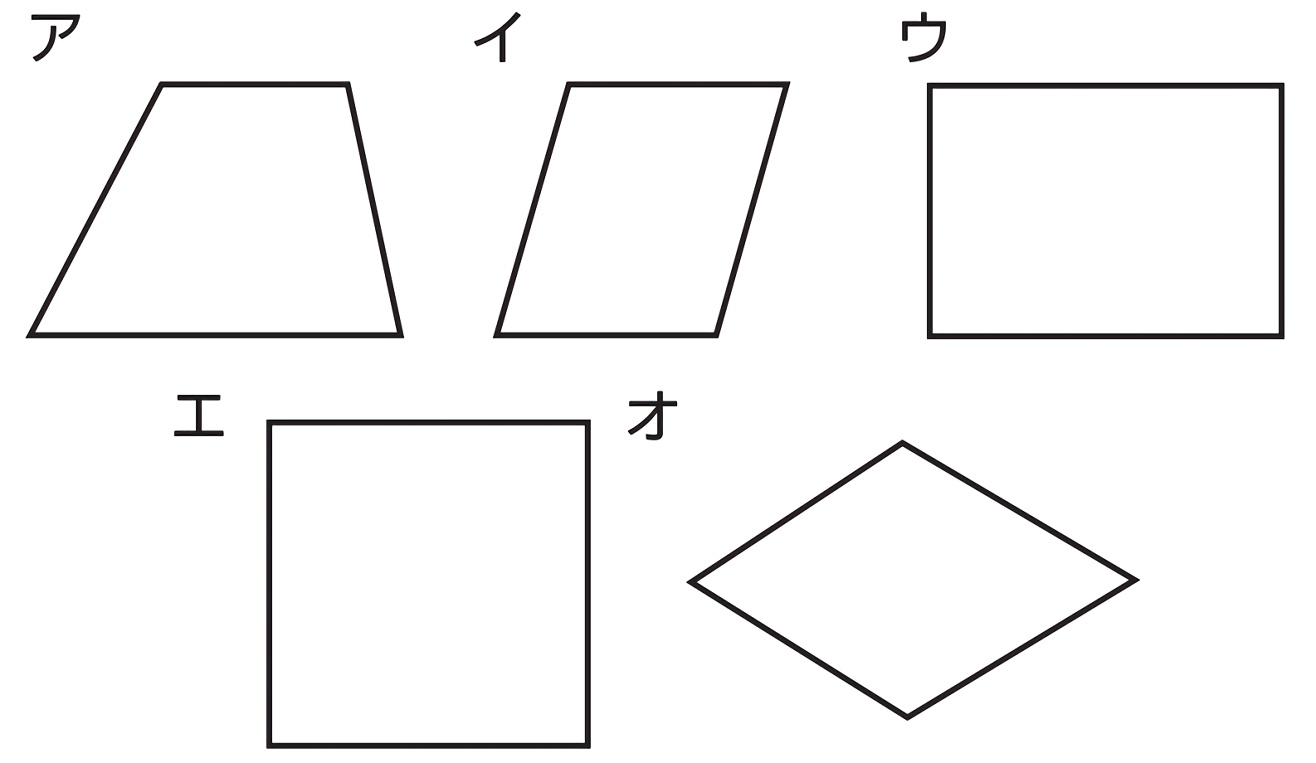



小6算数 多角形と対称 指導アイデア みんなの教育技術



Www City Sapporo Jp Kyoiku Shido Documents 1 6 3 12 Pdf




算数 図工 図形の導入 対称な図形



Http Cms Nerima Tky Ed Jp Weblog Files 103 Doc Pdf



Www Nipec Nein Ed Jp Sc Risuu H21 H21suugaku 6mizuno Pdf




8 31まで おためし問題集特典つき 天才ドリル 平面図形が得意になる点描写 線対称 小学校全学年用 算数 考える力を育てる 認知工学 本 通販 Amazon



小学6年生で 何の為に 点対称な図形 を学習するのでしょうか 目でもの Yahoo 知恵袋



中学1年数学 幾何 の授業にて その2 Student Life Style 法政大学第二中 高等学校
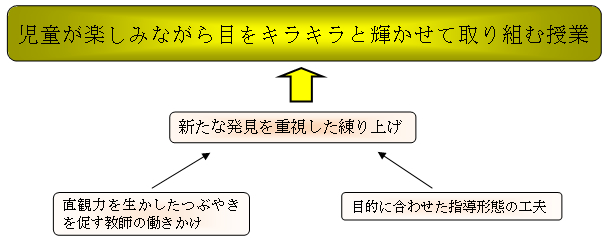



私の実践 私の工夫 算数 児童が楽しみながら目をキラキラと輝かせて取り組む授業を目指して 6年 対称な図形 啓林館




線対称



中1数学 点対称な図形とは まなビタミン



線対称と点対称1




世界一分かりやすい算数 小6 対称な図形




小6算数 対称な図形の折り紙 ブログ アビット
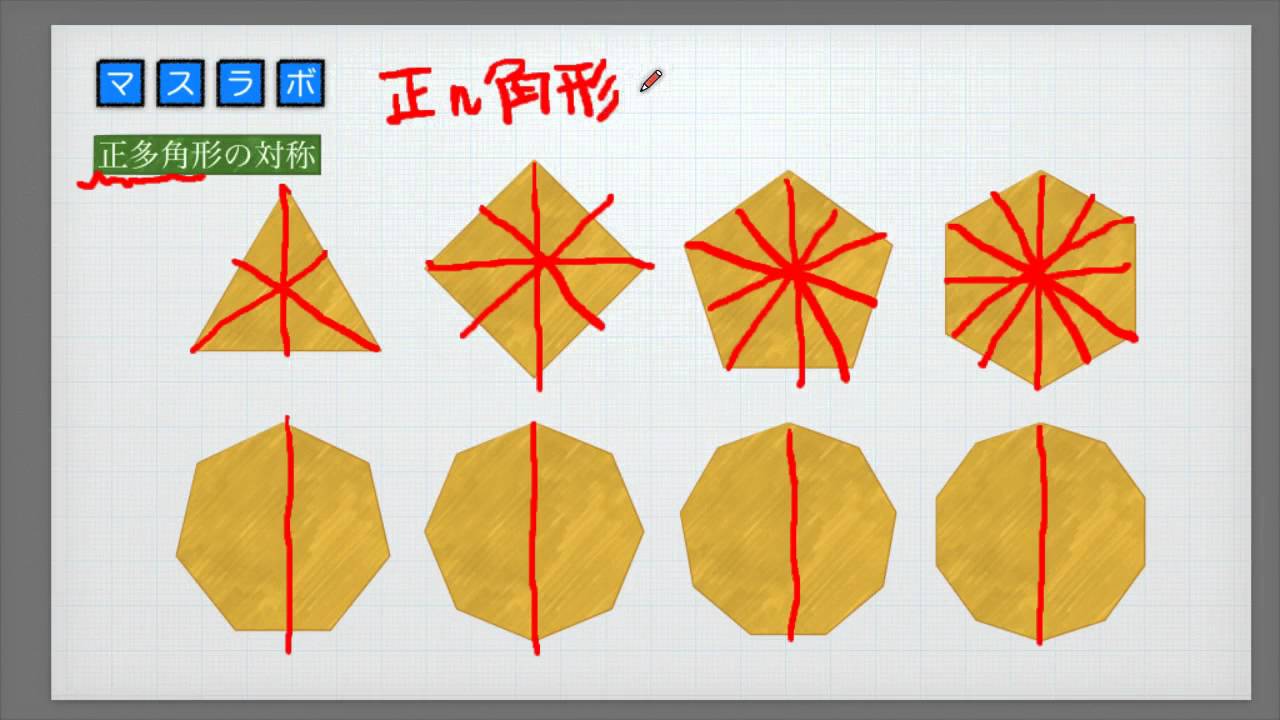



小学校6年生 算数 正多角形の対称 Youtube



線対称 算数解法の極意




私の実践 私の工夫 算数 児童が楽しみながら目をキラキラと輝かせて取り組む授業を目指して 6年 対称な図形 啓林館




小学校受験の対称図形の問題が苦手なお子さんは ここに注目して 折り紙図形 ゼロから始めた小学校受験合格までの道



Http Www Suginami School Ed Jp Hounanshou 11 6nenn Contact6 42sansu Pdf



幼児から折り紙で学ぶ線対称図形 点対称図形 成長している過程と結果が表れました 幼児からの思考力養成ブログ 幼児専門 さんすう塾のシナプス



Http Www2 Itc Kansai U Ac Jp Wakui Neckless Monkiri Slide Pdf



Math 点対称な図形のかき方 働きアリ The 2nd



6年生カテゴリの記事一覧 翁島 おきなしま 小学校ホームページ



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



Search Q E7 B9 E5 Af Be E7 B0 81 E5 9b E5 E4 B8 80 E8 A6 Tbm Isch



線対称と点対称2



Http Www2 Itc Kansai U Ac Jp Wakui Neckless Monkiri Slide Pdf



対称な図形と回転 桐朋中学 12年 どう解く 中学受験算数




折り紙で線対称




点対称と線対称はアルファベットで わくわく さんすう子育て 幼児さんすうインストラクター曽山桂子のブログ




6年算数 対称な図形 9時間目 いろいろな図形を対称の見方で調べよう Youtube




私の実践 私の工夫 算数 児童が楽しみながら目をキラキラと輝かせて取り組む授業を目指して 6年 対称な図形 啓林館



6年生カテゴリの記事一覧 翁島 おきなしま 小学校ホームページ



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ



1
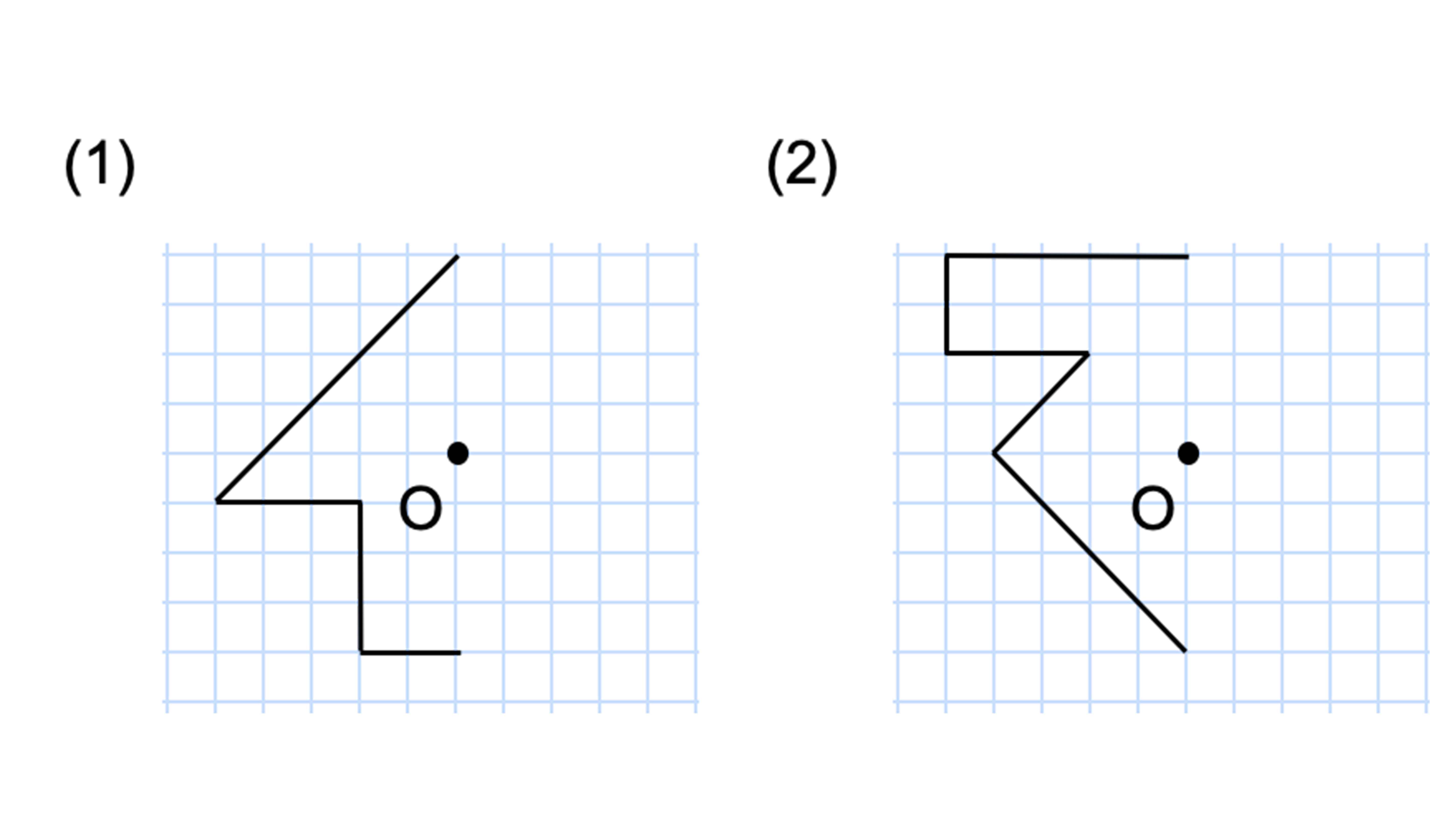



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
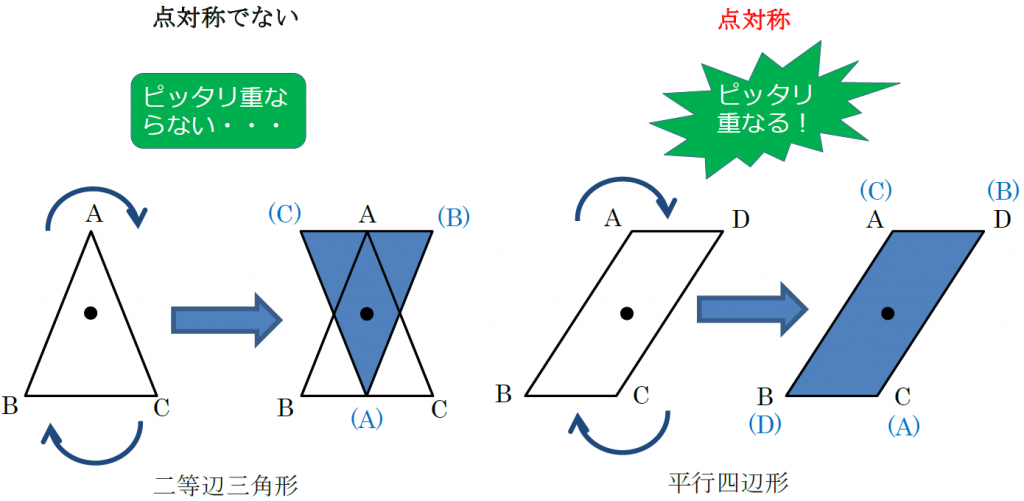



中1数学 点対称な図形とは まなビタミン




8 31まで おためし問題集特典つき おりがみで学ぶ図形パズル 小学校全学年用 算数 山口 榮一 本 通販 Amazon
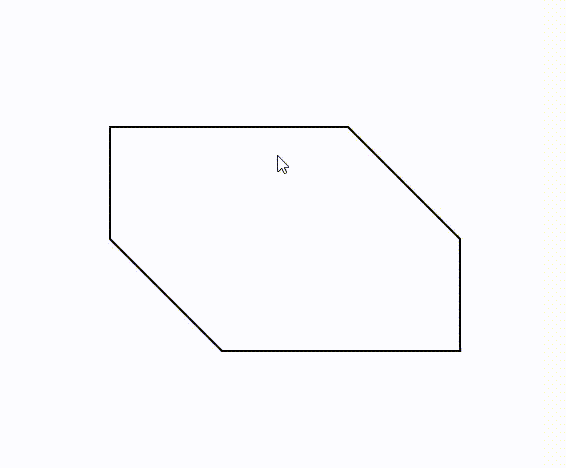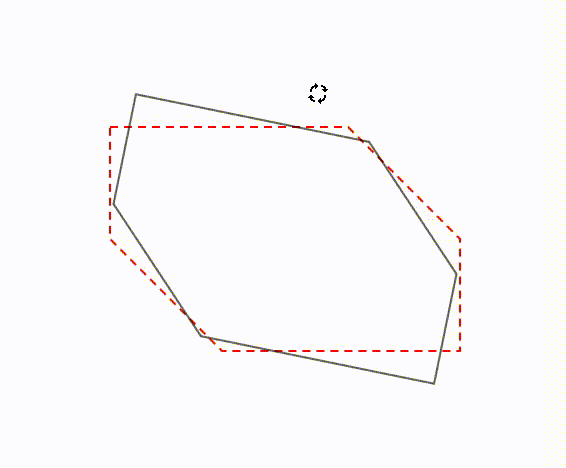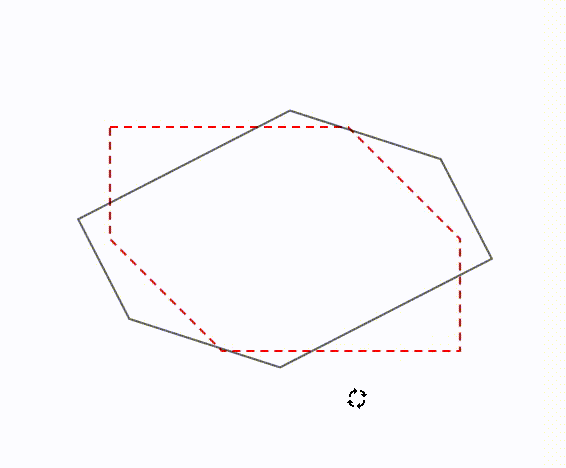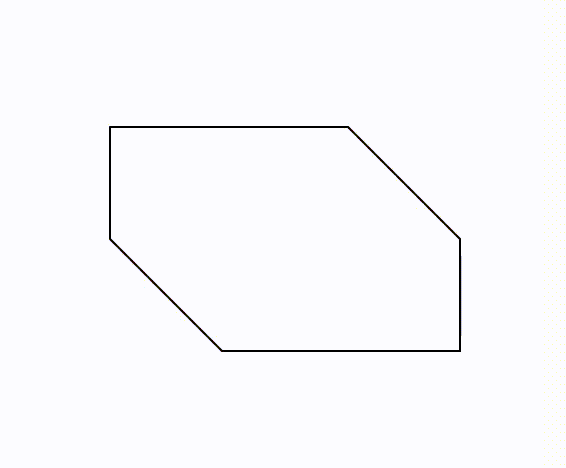



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun




6年生のみなさんへ 堀津小blog 羽島市立堀津小学校
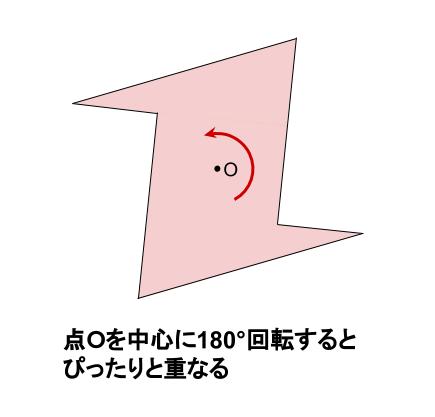



中学数学 点対称な図形 中学数学の無料オンライン学習サイトchu Su



6年算数 線対称な図形の理解は折り紙から 高岡市立国吉義務教育学校




線対称 に親しむ取り組み 3歳 6歳のレッスンで取り入れている4種 おうちで知育



中学1年数学 幾何 の授業にて その2 Student Life Style 法政大学第二中 高等学校



点対称な図形




8 31まで おためし問題集特典つき おりがみで学ぶ図形パズル 小学校全学年用 算数 山口 榮一 本 通販 Amazon



6年生カテゴリの記事一覧 翁島 おきなしま 小学校ホームページ



Www City Sapporo Jp Kyoiku Shido Documents 1 6 3 12 Pdf
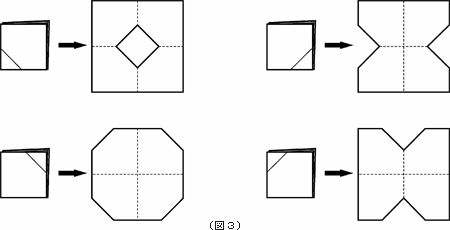



今何を学習すべきか 目次 こぐま会 幼児教育実践研究所




切り紙は絵が苦手でも作れた 子どもとカンタン工作しよう 銭屋工芸社
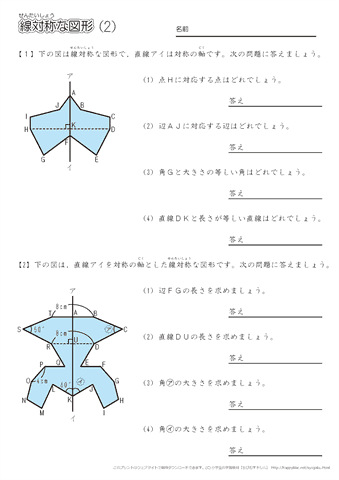



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生




小6 対称な図形 四角形 日本語版 Youtube



Www Nipec Nein Ed Jp Sc Risuu H21 H21suugaku 6mizuno Pdf




小6算数 対称な図形の折り紙 ブログ アビット




6年生のみなさんへ 堀津小blog 羽島市立堀津小学校



点対称の簡単な書き方を教えてください 逆さまにした時に同じに見えるこ Yahoo 知恵袋



Www Gakuto Co Jp Docs Ps Sansu Pdf Nenoshi27 6n A All Pdf




8 31まで おためし問題集特典つき おりがみで学ぶ図形パズル 小学校全学年用 算数 山口 榮一 本 通販 Amazon




算数のお勉強 になる前に 線対称な図形 で楽しくお遊び 2歳児からの考える力を伸ばす幼児教室 英才アカデミー東灘教室



幼児から折り紙で学ぶ線対称図形 点対称図形 成長している過程と結果が表れました 幼児からの思考力養成ブログ 幼児専門 さんすう塾のシナプス



幼児から折り紙で学ぶ線対称図形 点対称図形 成長している過程と結果が表れました 幼児からの思考力養成ブログ 幼児専門 さんすう塾のシナプス




よしまさ En Twitter H30奈良県公立高校入試から正方形の折り紙を題材にした対称な図形の問題です 問題文の情報を整理して相似な関係 三平方の定理を使います 後半が結構難しいです 後半は受験生の正答率わずか5 です 中学数学




6年生で学習する 対称 なんですが この形は点対称ですか 線対称ですか Clear



折り紙線対称 Wormo ワーモ
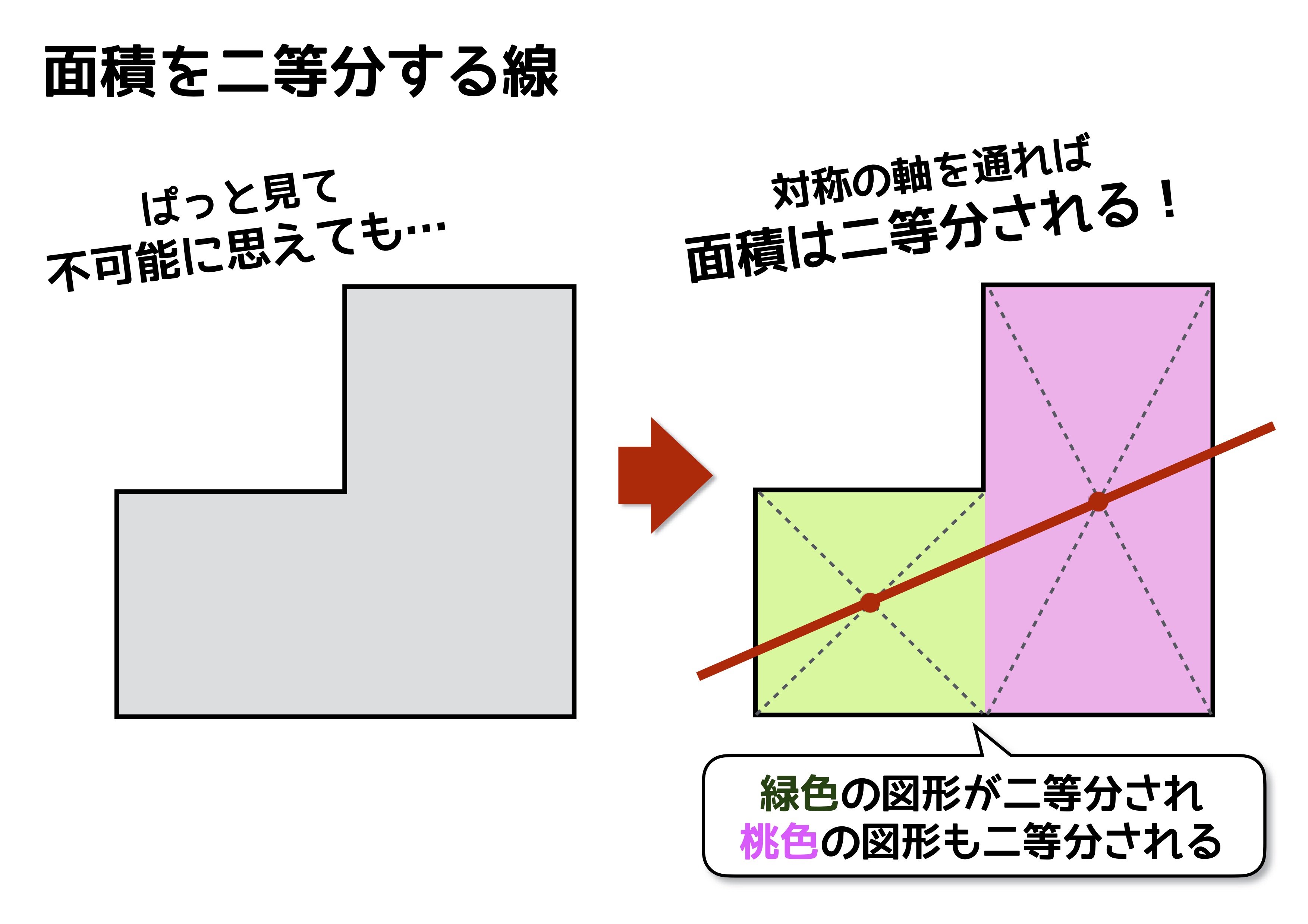



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ




公立中高一貫が良く出題する折り紙問題 オンライン授業専門塾ファイ
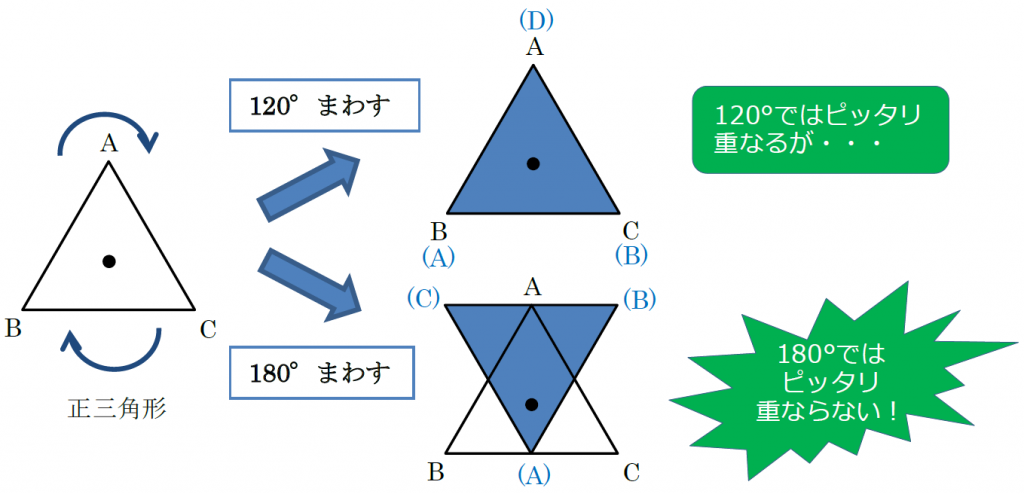



中1数学 点対称な図形とは まなビタミン



実践例 プログラミングで対称な図形を学ぶ 山崎智仁 Tomohito Yamazaki Note




折り紙で6角形の図形を2種類作ってみよう




おりがみ大図鑑 こちら 宝石みたいな形で 点対称 線対称 Facebook



対称な図形と授業運営 教育考現学




折り紙で線対称



Http Cms Nerima Tky Ed Jp Weblog Files 103 Doc Pdf



6年生カテゴリの記事一覧 翁島 おきなしま 小学校ホームページ



多角形と対称 6年生 翁島 おきなしま 小学校ホームページ



Http Www Hidaka Ed Jp Msd Es Mondaisyuu Gakuryokukoujou Sansuu 06tousyo Kaitou Pdf




小学校受験の線対称 対称図形の問題につまずいたら折り紙を使おう 小学生 中学生になっても役に立つ ゼロから始めた小学校受験合格までの道



Http Www Suginami School Ed Jp Hounanshou 11 6nenn Contact6 42sansu Pdf



線対称図形と点対称図形の見分け方 算数解法の極意
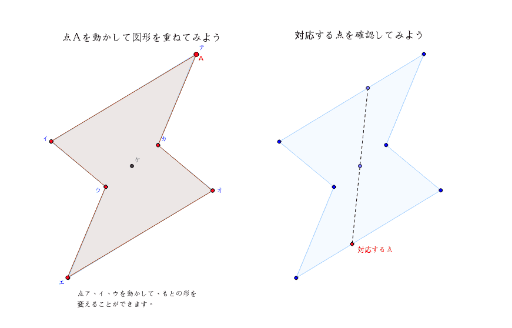



点対称な図形の観察 Geogebra
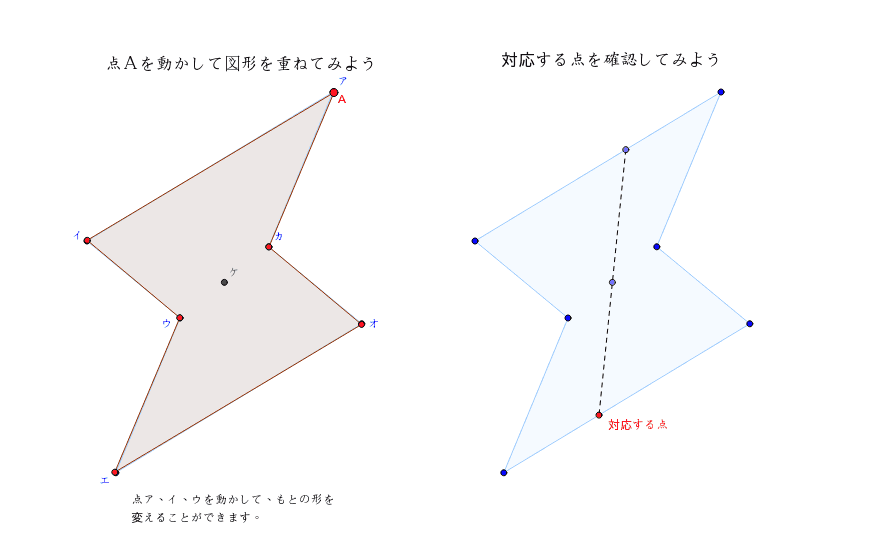



点対称な図形の観察 Geogebra
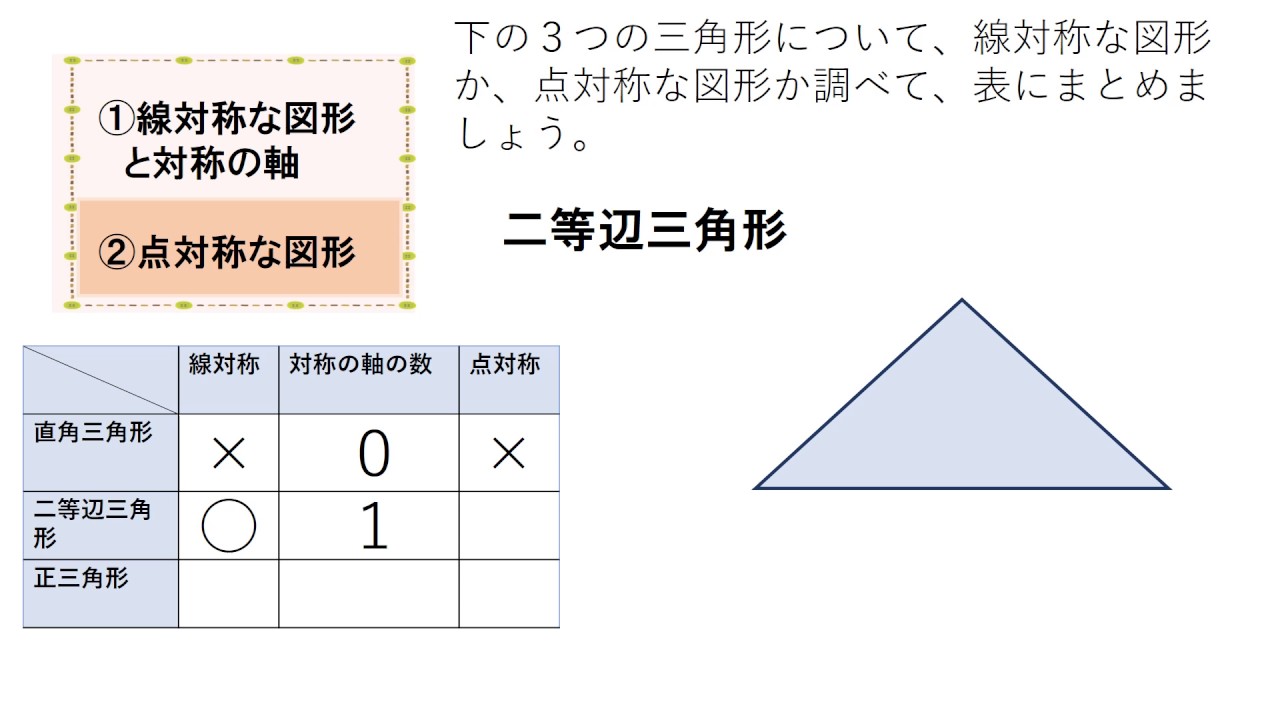



小6 対称な図形 三角形 日本語版 Youtube




スマホok 6年 対称な図形 多角形と対称 Youtube



1
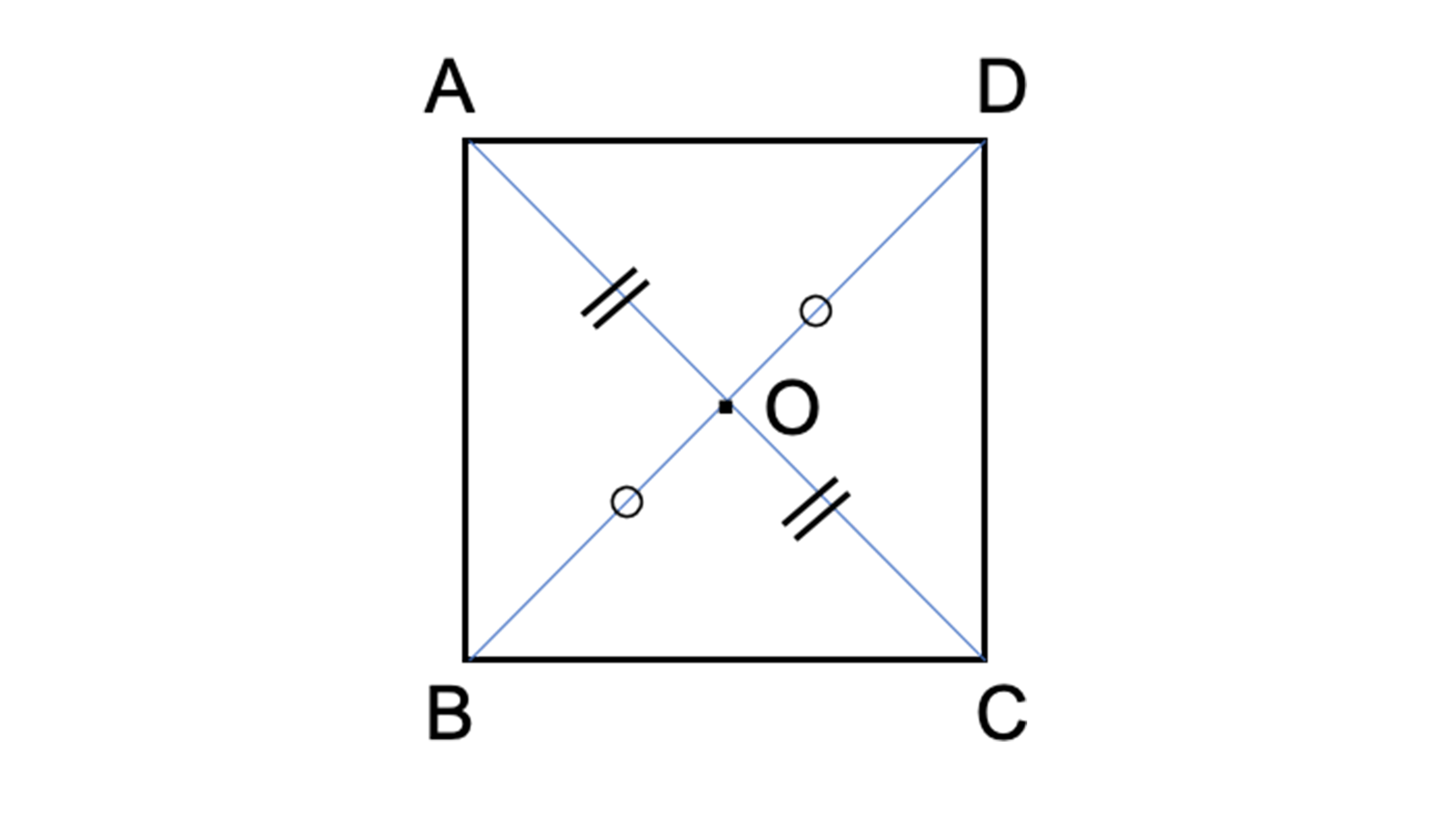



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
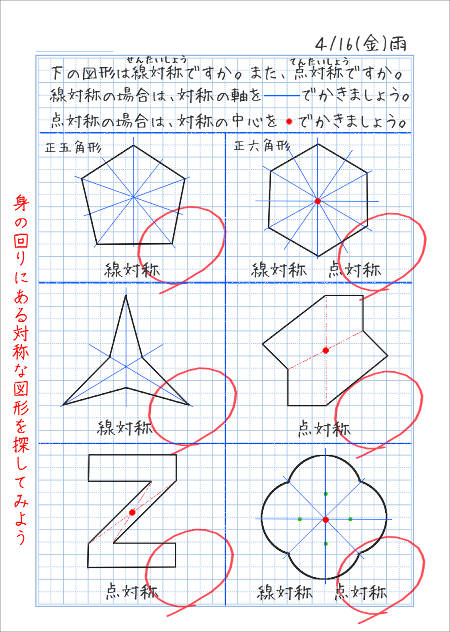



線対称と点対称の自主学習ノート 家庭学習レシピ



0 件のコメント:
コメントを投稿